Question Number 27840 by bmind4860 last updated on 15/Jan/18
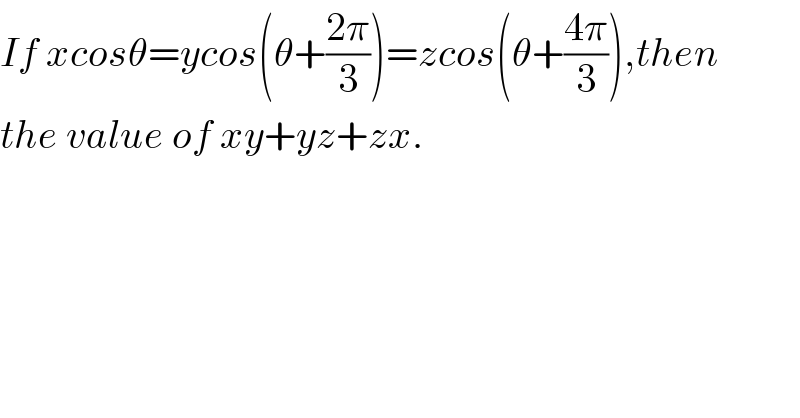
$${If}\:{xcos}\theta={ycos}\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)={zcos}\left(\theta+\frac{\mathrm{4}\pi}{\mathrm{3}}\right),{then} \\ $$$${the}\:{value}\:{of}\:{xy}+{yz}+{zx}. \\ $$
Answered by ajfour last updated on 15/Jan/18
![let xcos θ=ycos (θ+((2π)/3)) =zcos (θ+((4π)/3))=r xy+yz+zx=xyz((1/x)+(1/y)+(1/z)) =(r^3 /(cos θcos (θ+((2π)/3))cos (θ+((4π)/3))))[((cos θ)/r)+((cos (θ+((2π)/3)))/r)+((cos (θ+((4π)/3)))/r)] and since cos θ+cos (θ+((4π)/3))+cos (θ+((2π)/3)) =2cos (θ+((2π)/3))cos (((2π)/3))+cos (θ+((2π)/3)) =−cos (θ+((2π)/3))+cos (θ+((2π)/3))=0 so xy+yz+zx=0 .](https://www.tinkutara.com/question/Q27849.png)
$${let}\:\:\:\:{x}\mathrm{cos}\:\theta={y}\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={z}\mathrm{cos}\:\left(\theta+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)={r}\: \\ $$$${xy}+{yz}+{zx}={xyz}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}}+\frac{\mathrm{1}}{{z}}\right) \\ $$$$\:\:\:\:=\frac{{r}^{\mathrm{3}} }{\mathrm{cos}\:\theta\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\mathrm{cos}\:\left(\theta+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)}\left[\frac{\mathrm{cos}\:\theta}{{r}}+\frac{\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)}{{r}}+\frac{\mathrm{cos}\:\left(\theta+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)}{{r}}\right] \\ $$$${and}\:{since} \\ $$$$\mathrm{cos}\:\theta+\mathrm{cos}\:\left(\theta+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)+\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$=\mathrm{2cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)\mathrm{cos}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right) \\ $$$$=−\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)+\mathrm{cos}\:\left(\theta+\frac{\mathrm{2}\pi}{\mathrm{3}}\right)=\mathrm{0} \\ $$$${so}\:\:\:\boldsymbol{{xy}}+\boldsymbol{{yz}}+\boldsymbol{{zx}}=\mathrm{0}\:. \\ $$
Commented by bmind4860 last updated on 15/Jan/18

$${superb}!\:{sir} \\ $$
