Question Number 34647 by JOHNMASANJA last updated on 09/May/18
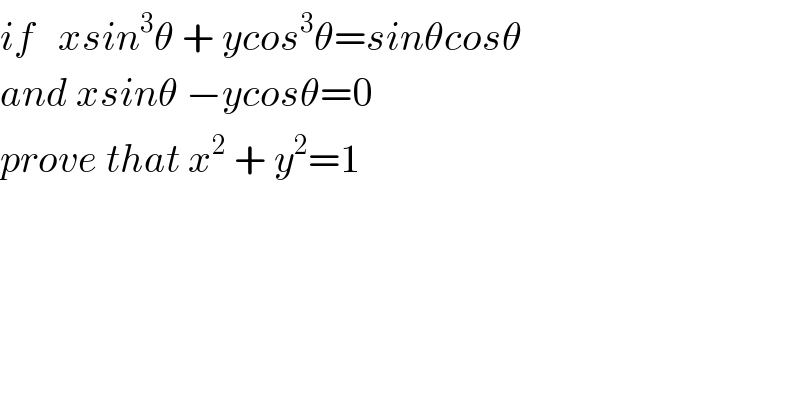
$${if}\:\:\:{xsin}^{\mathrm{3}} \theta\:+\:{ycos}^{\mathrm{3}} \theta={sin}\theta{cos}\theta \\ $$$${and}\:{xsin}\theta\:−{ycos}\theta=\mathrm{0} \\ $$$${prove}\:{that}\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} =\mathrm{1} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 09/May/18

$${xsin}\theta={ycos}\theta \\ $$$$\frac{{x}}{{cos}\theta}=\frac{{y}}{{sin}\theta}={k}\left({assumed}\right) \\ $$$${x}={kcos}\theta\:,{y}={ksin}\theta \\ $$$${putting}\:{in}\:{first}\:{equation}\:\: \\ $$$${kcos}\theta{sin}^{\mathrm{3}} \theta+{ksin}\theta{cos}^{\mathrm{3}} \theta={sin}\theta{cos}\theta \\ $$$${ksin}\theta{cos}\theta\left({sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta\right)={sin}\theta{cos}\theta \\ $$$${so}\:{k}=\mathrm{1} \\ $$$${hence}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} \\ $$$$={cos}^{\mathrm{2}} \theta+{sin}^{\mathrm{2}} \theta \\ $$$$=\mathrm{1} \\ $$
Answered by ajfour last updated on 09/May/18
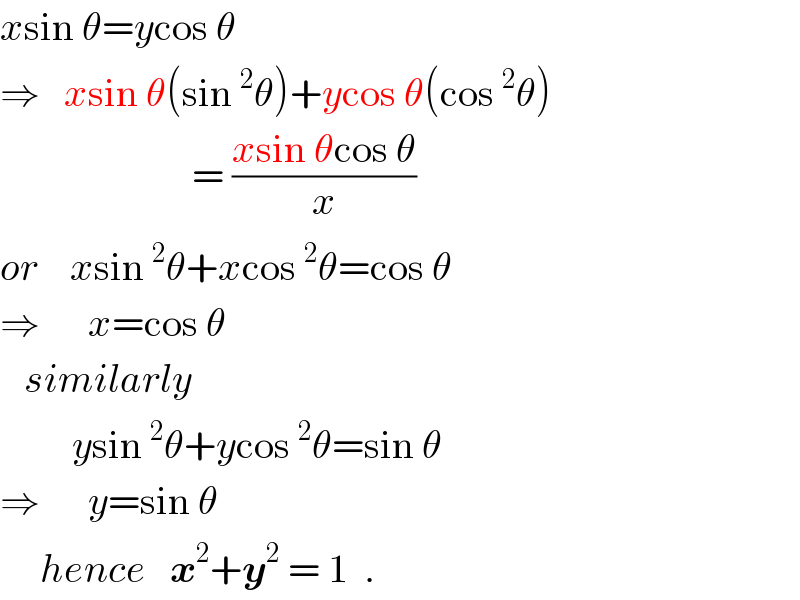
$${x}\mathrm{sin}\:\theta={y}\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\:{x}\mathrm{sin}\:\theta\left(\mathrm{sin}\:^{\mathrm{2}} \theta\right)+{y}\mathrm{cos}\:\theta\left(\mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{{x}\mathrm{sin}\:\theta\mathrm{cos}\:\theta}{{x}} \\ $$$${or}\:\:\:\:{x}\mathrm{sin}\:^{\mathrm{2}} \theta+{x}\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{cos}\:\theta \\ $$$$\Rightarrow\:\:\:\:\:\:{x}=\mathrm{cos}\:\theta \\ $$$$\:\:\:{similarly} \\ $$$$\:\:\:\:\:\:\:\:\:{y}\mathrm{sin}\:^{\mathrm{2}} \theta+{y}\mathrm{cos}\:^{\mathrm{2}} \theta=\mathrm{sin}\:\theta \\ $$$$\Rightarrow\:\:\:\:\:\:{y}=\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:{hence}\:\:\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \:=\:\mathrm{1}\:\:. \\ $$
