Question Number 127477 by ZiYangLee last updated on 30/Dec/20
![If y=(1/(x(1−x))), show that (d^n y/dx^n )=n![(((−1)^n )/x^(n+1) )+(1/((1−x)^(n+1) ))]](https://www.tinkutara.com/question/Q127477.png)
$$\mathrm{If}\:{y}=\frac{\mathrm{1}}{{x}\left(\mathrm{1}−{x}\right)}, \\ $$$$\mathrm{show}\:\mathrm{that}\:\frac{{d}^{{n}} {y}}{{dx}^{{n}} }={n}!\left[\frac{\left(−\mathrm{1}\right)^{{n}} }{{x}^{{n}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} }\right] \\ $$
Answered by Dwaipayan Shikari last updated on 30/Dec/20
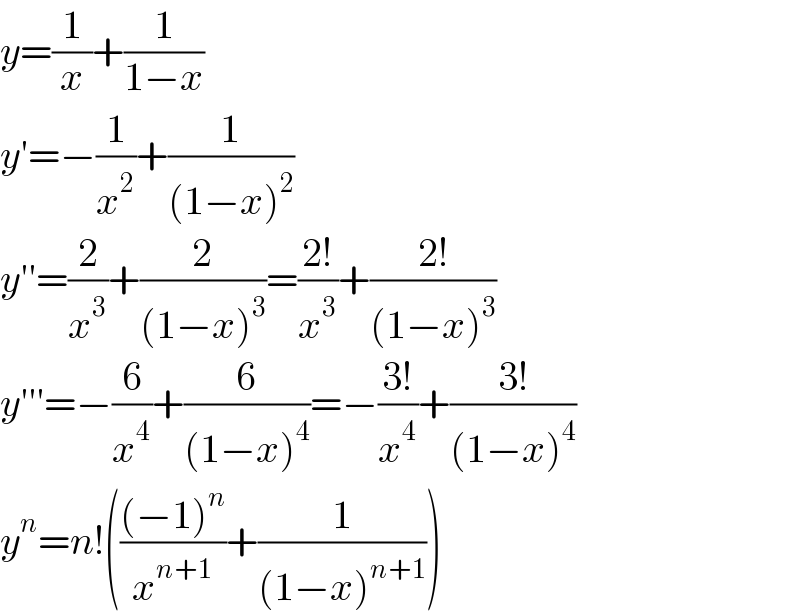
$${y}=\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${y}'=−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${y}''=\frac{\mathrm{2}}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\frac{\mathrm{2}!}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}!}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${y}'''=−\frac{\mathrm{6}}{{x}^{\mathrm{4}} }+\frac{\mathrm{6}}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=−\frac{\mathrm{3}!}{{x}^{\mathrm{4}} }+\frac{\mathrm{3}!}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} } \\ $$$${y}^{{n}} ={n}!\left(\frac{\left(−\mathrm{1}\right)^{{n}} }{{x}^{{n}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{{n}+\mathrm{1}} }\right) \\ $$
