Question Number 97818 by I want to learn more last updated on 09/Jun/20
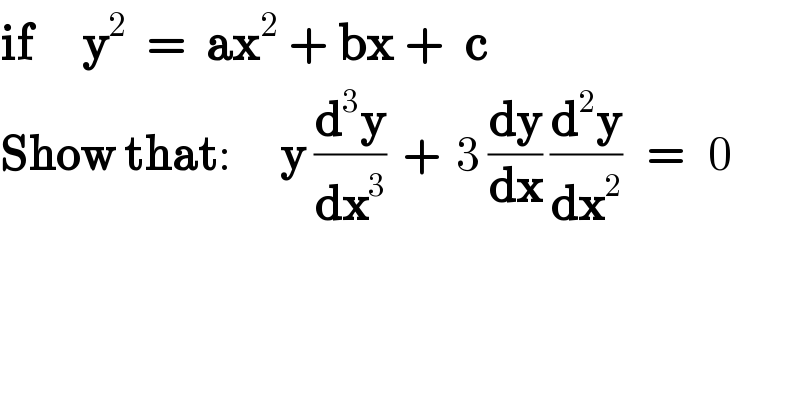
$$\boldsymbol{\mathrm{if}}\:\:\:\:\:\boldsymbol{\mathrm{y}}^{\mathrm{2}} \:\:=\:\:\boldsymbol{\mathrm{ax}}^{\mathrm{2}} \:+\:\boldsymbol{\mathrm{bx}}\:+\:\:\boldsymbol{\mathrm{c}} \\ $$$$\boldsymbol{\mathrm{Show}}\:\boldsymbol{\mathrm{that}}:\:\:\:\:\:\:\boldsymbol{\mathrm{y}}\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{3}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{3}} }\:\:+\:\:\mathrm{3}\:\frac{\boldsymbol{\mathrm{dy}}}{\boldsymbol{\mathrm{dx}}}\:\frac{\boldsymbol{\mathrm{d}}^{\mathrm{2}} \boldsymbol{\mathrm{y}}}{\boldsymbol{\mathrm{dx}}^{\mathrm{2}} }\:\:\:=\:\:\:\mathrm{0} \\ $$
Answered by Rio Michael last updated on 09/Jun/20
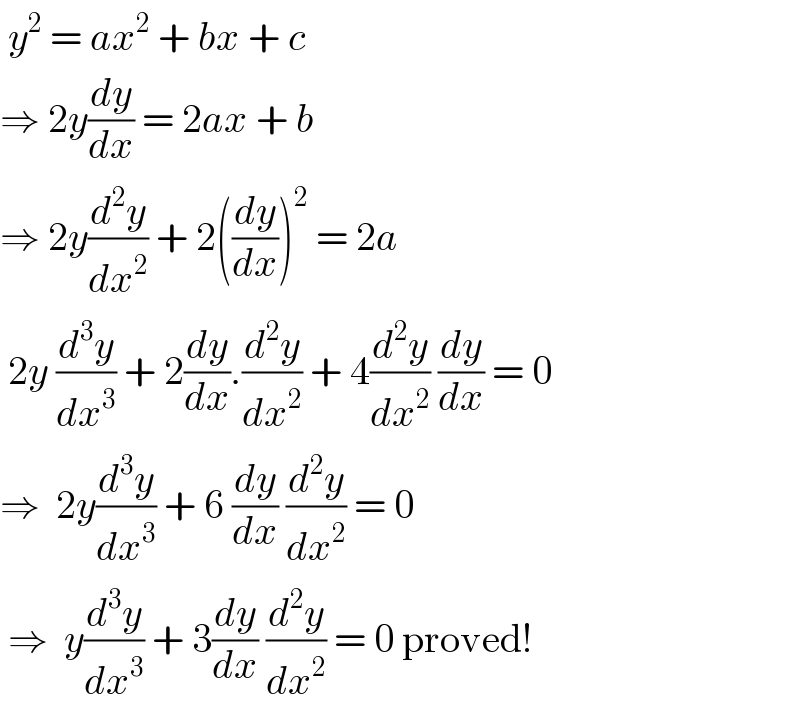
$$\:{y}^{\mathrm{2}} \:=\:{ax}^{\mathrm{2}} \:+\:{bx}\:+\:{c} \\ $$$$\Rightarrow\:\mathrm{2}{y}\frac{{dy}}{{dx}}\:=\:\mathrm{2}{ax}\:+\:{b} \\ $$$$\Rightarrow\:\mathrm{2}{y}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{2}\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:=\:\mathrm{2}{a}\: \\ $$$$\:\mathrm{2}{y}\:\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }\:+\:\mathrm{2}\frac{{dy}}{{dx}}.\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{4}\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:\frac{{dy}}{{dx}}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{2}{y}\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }\:+\:\mathrm{6}\:\frac{{dy}}{{dx}}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\mathrm{0} \\ $$$$\:\Rightarrow\:\:{y}\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }\:+\:\mathrm{3}\frac{{dy}}{{dx}}\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:=\:\mathrm{0}\:\mathrm{proved}! \\ $$
Commented by I want to learn more last updated on 09/Jun/20

$$\mathrm{Thanks}\:\mathrm{sir} \\ $$
