Question Number 37915 by gunawan last updated on 19/Jun/18
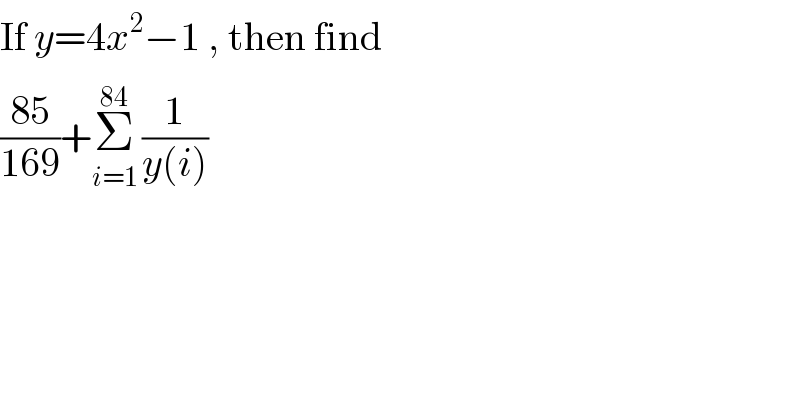
$$\mathrm{If}\:{y}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{1}\:,\:\mathrm{then}\:\mathrm{find} \\ $$$$\frac{\mathrm{85}}{\mathrm{169}}+\underset{{i}=\mathrm{1}} {\overset{\mathrm{84}} {\Sigma}}\:\frac{\mathrm{1}}{{y}\left({i}\right)}\: \\ $$
Answered by ajfour last updated on 19/Jun/18
![S−((85)/(169))=Σ_(r=1) ^(84) (1/((2r−1)(2r+1))) =(1/2)Σ_(r=1) ^(84) [(((2r+1)−(2r−1))/((2r−1)(2r+1)))] =(1/2)Σ_(r=1) ^(84) [(1/(2r−1))−(1/(2r+1))] =(1/2)((1/1)−(1/3)+(1/3)−(1/5)+...+(1/(167))−(1/(169))) S=((85)/(169))−(1/2)(1−(1/(169))) = (1/(169)) .](https://www.tinkutara.com/question/Q37918.png)
$${S}−\frac{\mathrm{85}}{\mathrm{169}}=\underset{{r}=\mathrm{1}} {\overset{\mathrm{84}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{r}−\mathrm{1}\right)\left(\mathrm{2}{r}+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{84}} {\sum}}\left[\frac{\left(\mathrm{2}{r}+\mathrm{1}\right)−\left(\mathrm{2}{r}−\mathrm{1}\right)}{\left(\mathrm{2}{r}−\mathrm{1}\right)\left(\mathrm{2}{r}+\mathrm{1}\right)}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\underset{{r}=\mathrm{1}} {\overset{\mathrm{84}} {\sum}}\left[\frac{\mathrm{1}}{\mathrm{2}{r}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{r}+\mathrm{1}}\right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+…+\frac{\mathrm{1}}{\mathrm{167}}−\frac{\mathrm{1}}{\mathrm{169}}\right) \\ $$$${S}=\frac{\mathrm{85}}{\mathrm{169}}−\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{169}}\right)\:=\:\frac{\mathrm{1}}{\mathrm{169}}\:. \\ $$
Commented by gunawan last updated on 19/Jun/18
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir} \\ $$$$ \\ $$
