Question Number 35642 by rahul 19 last updated on 21/May/18
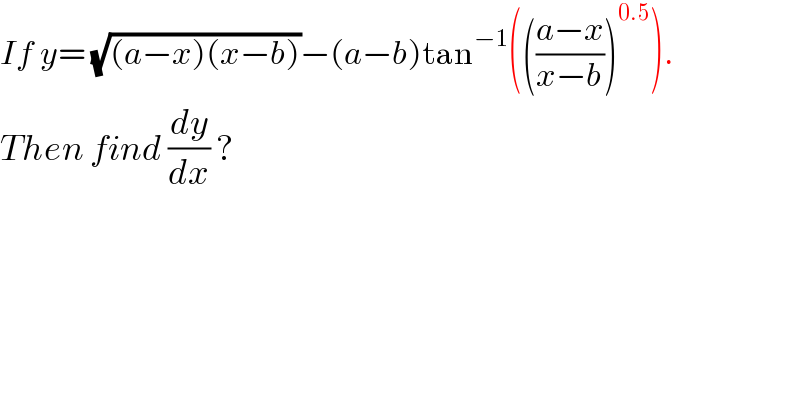
$${If}\:{y}=\:\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}−\left({a}−{b}\right)\mathrm{tan}^{−\mathrm{1}} \left(\left(\frac{{a}−{x}}{{x}−{b}}\right)^{\mathrm{0}.\mathrm{5}} \right). \\ $$$${Then}\:{find}\:\frac{{dy}}{{dx}}\:? \\ $$
Commented by rahul 19 last updated on 21/May/18
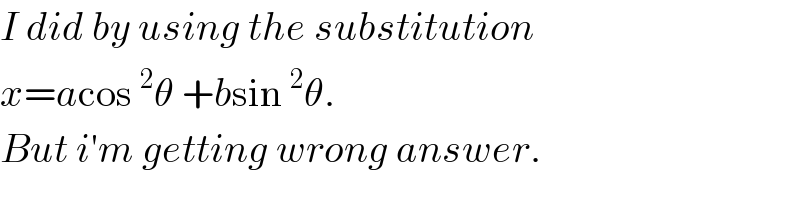
$${I}\:{did}\:{by}\:{using}\:{the}\:{substitution} \\ $$$${x}={a}\mathrm{cos}\:^{\mathrm{2}} \theta\:+{b}\mathrm{sin}\:^{\mathrm{2}} \theta.\: \\ $$$${But}\:{i}'{m}\:{getting}\:{wrong}\:{answer}. \\ $$
Commented by abdo imad last updated on 21/May/18

$${we}\:{have}\:{y}\left({x}\right)=\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}\:−\left({a}−{b}\right){arctan}\left(\sqrt{\frac{{a}−{x}}{{x}−{b}}}\:\right) \\ $$$${y}\left({x}\right)\:=\sqrt{{u}\left({x}\right)}\:\:−\left({a}−{b}\right){arctan}\:\left({v}\left({x}\right)\right)\:\Rightarrow \\ $$$${y}^{'} \left({x}\right)\:=\:\frac{{u}^{'} \left({x}\right)}{\mathrm{2}\sqrt{{u}\left({x}\right)}}\:\:−\left({a}−{b}\right)\:\frac{{v}^{'} \left({x}\right)}{\mathrm{1}+{v}^{\mathrm{2}} \left({x}\right)}\:\:{but}\:{we}\:{have} \\ $$$${u}^{'} \left({x}\right)=−\left({x}−{b}\right)\:+{a}−{x}\:=\:−\mathrm{2}{x}\:+{a}+{b}\:\:\:\:\:\:\:\mid_{\mathrm{1}} ^{−\mathrm{1}} \\ $$$${v}^{'} \left({x}\right)=\:\frac{\left(\frac{{a}−{x}}{{x}−{b}}\right)^{'} }{\mathrm{2}\sqrt{\frac{{a}−{x}}{{x}−{b}}}}\:=\:\frac{−\left({x}−{b}\right)−\left({a}−{x}\right)}{\left({x}−{b}\right)^{\mathrm{2}} \:\:\mathrm{2}\:.\sqrt{\frac{{a}−{x}}{{x}−{b}}}}\:=\:\frac{{b}−{a}}{\mathrm{2}\left({x}−{b}\right)^{\mathrm{2}} \frac{\sqrt{{a}−{x}_{} }}{\:\sqrt{{x}−{b}}}} \\ $$$$=\:\frac{{b}−{a}}{\mathrm{2}\left(\sqrt{{x}−{b}}\right)^{\mathrm{3}} \sqrt{{a}−{x}}}\:\Rightarrow \\ $$$${y}^{'} \left({x}\right)\:=\:\frac{−\mathrm{2}{x}\:+{a}+{b}}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}}\:\:+\:\:\:\:\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{{a}−{x}}\left(\sqrt{{x}−{b}}\right)^{\mathrm{3}} }\:×\:\frac{\mathrm{1}}{\mathrm{1}+\frac{{a}−{x}}{{x}−{b}}} \\ $$$$=\frac{−\mathrm{2}{x}\:+{a}+{b}}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}}\:\:+\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\frac{{x}−{b}}{\mathrm{2}\sqrt{{a}−{x}}\left({x}−{b}\right)\sqrt{{x}−{b}}\left({a}−{b}\right)} \\ $$$$=\frac{−\mathrm{2}{ax}\:+{a}+{b}}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}}\:\:+\:\:\:\:\:\:\frac{{a}−{b}}{\mathrm{4}\sqrt{{a}−{x}}\sqrt{{x}−{b}}}\:. \\ $$
Answered by ajfour last updated on 21/May/18
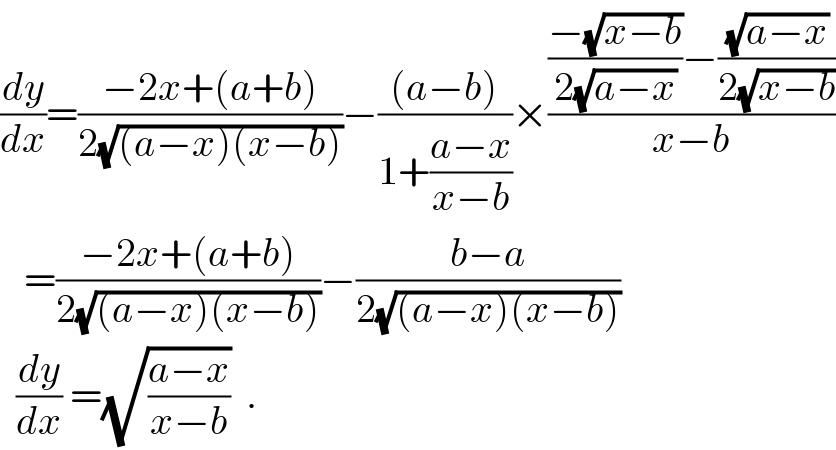
$$\frac{{dy}}{{dx}}=\frac{−\mathrm{2}{x}+\left({a}+{b}\right)}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}}−\frac{\left({a}−{b}\right)}{\mathrm{1}+\frac{{a}−{x}}{{x}−{b}}}×\frac{\frac{−\sqrt{{x}−{b}}}{\mathrm{2}\sqrt{{a}−{x}}}−\frac{\sqrt{{a}−{x}}}{\mathrm{2}\sqrt{{x}−{b}}}}{{x}−{b}} \\ $$$$\:\:\:=\frac{−\mathrm{2}{x}+\left({a}+{b}\right)}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}}−\frac{{b}−{a}}{\mathrm{2}\sqrt{\left({a}−{x}\right)\left({x}−{b}\right)}} \\ $$$$\:\:\frac{{dy}}{{dx}}\:=\sqrt{\frac{{a}−{x}}{{x}−{b}}}\:\:. \\ $$
Commented by rahul 19 last updated on 21/May/18

$${Thank}\:{you}\:{sir}. \\ $$
