Menu Close

If-y-n-1-y-n-6-and-y-0-7-Find-y-n-

Tinku Tara 0 Comments
Pin




Question Number 95014 by I want to learn more last updated on 22/May/20
If y_(n + 1) − y_n = 6, and y_0 = 7 Find y_n
$$\boldsymbol{\mathrm{If}}\:\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}\:\:+\:\:\mathrm{1}} \:\:−\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}} \:\:\:=\:\:\:\mathrm{6},\:\:\:\:\:\:\:\boldsymbol{\mathrm{and}}\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\mathrm{0}} \:\:=\:\:\:\mathrm{7} \\ $$$$\boldsymbol{\mathrm{Find}}\:\:\:\:\:\boldsymbol{\mathrm{y}}_{\boldsymbol{\mathrm{n}}} \\ $$
Commented by prakash jain last updated on 22/May/20
This is an arithmetic progression: y_0 =7 y_(n+1) =y_n +6 firzt term 7 common difference=6 y_n =7+n6
$$\mathrm{This}\:\mathrm{is}\:\mathrm{an}\:\mathrm{arithmetic}\:\mathrm{progression}: \\ $$$${y}_{\mathrm{0}} =\mathrm{7} \\ $$$${y}_{{n}+\mathrm{1}} ={y}_{{n}} +\mathrm{6} \\ $$$$\mathrm{firzt}\:\mathrm{term}\:\mathrm{7} \\ $$$$\mathrm{common}\:\mathrm{difference}=\mathrm{6} \\ $$$${y}_{{n}} =\mathrm{7}+{n}\mathrm{6} \\ $$
Commented by I want to learn more last updated on 22/May/20
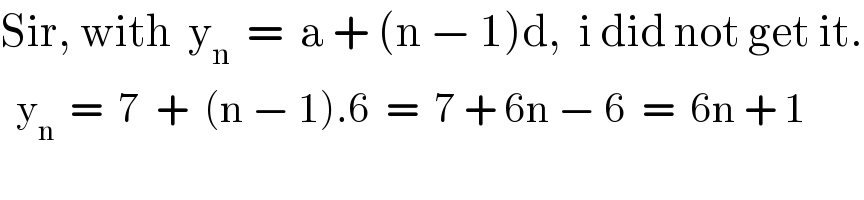
Sir, with y_n = a + (n − 1)d, i did not get it. y_n = 7 + (n − 1).6 = 7 + 6n − 6 = 6n + 1
$$\mathrm{Sir},\:\mathrm{with}\:\:\mathrm{y}_{\mathrm{n}} \:\:=\:\:\mathrm{a}\:+\:\left(\mathrm{n}\:−\:\mathrm{1}\right)\mathrm{d},\:\:\mathrm{i}\:\mathrm{did}\:\mathrm{not}\:\mathrm{get}\:\mathrm{it}. \\ $$$$\:\:\mathrm{y}_{\mathrm{n}} \:\:=\:\:\mathrm{7}\:\:+\:\:\left(\mathrm{n}\:−\:\mathrm{1}\right).\mathrm{6}\:\:=\:\:\mathrm{7}\:+\:\mathrm{6n}\:−\:\mathrm{6}\:\:=\:\:\mathrm{6n}\:+\:\mathrm{1} \\ $$
Commented by I want to learn more last updated on 22/May/20
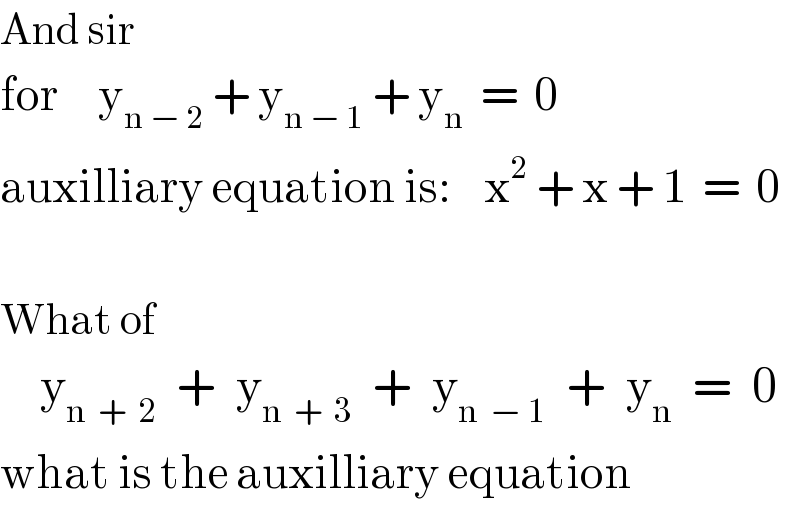
And sir for y_(n − 2) + y_(n − 1) + y_n = 0 auxilliary equation is: x^2 + x + 1 = 0 What of y_(n + 2) + y_(n + 3) + y_(n − 1) + y_n = 0 what is the auxilliary equation
$$\mathrm{And}\:\mathrm{sir} \\ $$$$\mathrm{for}\:\:\:\:\:\mathrm{y}_{\mathrm{n}\:−\:\mathrm{2}} \:+\:\mathrm{y}_{\mathrm{n}\:−\:\mathrm{1}} \:+\:\mathrm{y}_{\mathrm{n}} \:\:=\:\:\mathrm{0} \\ $$$$\mathrm{auxilliary}\:\mathrm{equation}\:\mathrm{is}:\:\:\:\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{x}\:+\:\mathrm{1}\:\:=\:\:\mathrm{0} \\ $$$$ \\ $$$$\mathrm{What}\:\mathrm{of} \\ $$$$\:\:\:\:\mathrm{y}_{\mathrm{n}\:\:+\:\:\mathrm{2}} \:\:+\:\:\mathrm{y}_{\mathrm{n}\:\:+\:\:\mathrm{3}} \:\:+\:\:\mathrm{y}_{\mathrm{n}\:\:−\:\mathrm{1}} \:\:+\:\:\mathrm{y}_{\mathrm{n}} \:\:=\:\:\mathrm{0} \\ $$$$\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{auxilliary}\:\mathrm{equation} \\ $$
Commented by mr W last updated on 22/May/20
“you want to learn more” sir: try to learn things one after an other! if you are still at the level for AP, forget at first “auxilliary equation”. back to your original question: you should make clear what you mean with “n”. if you say y_n =6n+1, but you gave your first term y_0 , then you are wrong, since y_0 =6×0+1=1≠7. correct is y_n =6n+7. so never just learn a formula, but learn what is behind it!
$$“{you}\:{want}\:{to}\:{learn}\:{more}''\:{sir}: \\ $$$${try}\:{to}\:{learn}\:{things}\:{one}\:{after}\:{an}\:{other}! \\ $$$${if}\:{you}\:{are}\:{still}\:{at}\:{the}\:{level}\:{for}\:{AP}, \\ $$$${forget}\:{at}\:{first}\:“{auxilliary}\:{equation}''. \\ $$$${back}\:{to}\:{your}\:{original}\:{question}: \\ $$$${you}\:{should}\:{make}\:{clear}\:{what}\:{you}\:{mean} \\ $$$${with}\:“{n}''.\:{if}\:{you}\:{say}\:{y}_{{n}} =\mathrm{6}{n}+\mathrm{1},\:{but} \\ $$$${you}\:{gave}\:{your}\:{first}\:{term}\:{y}_{\mathrm{0}} ,\:{then} \\ $$$${you}\:{are}\:{wrong},\:{since}\:{y}_{\mathrm{0}} =\mathrm{6}×\mathrm{0}+\mathrm{1}=\mathrm{1}\neq\mathrm{7}. \\ $$$${correct}\:{is}\:{y}_{{n}} =\mathrm{6}{n}+\mathrm{7}.\:{so}\:{never}\:{just} \\ $$$${learn}\:{a}\:{formula},\:{but}\:{learn}\:{what}\:{is} \\ $$$${behind}\:{it}! \\ $$
Commented by I want to learn more last updated on 22/May/20
Thanks sir.
$$\mathrm{Thanks}\:\mathrm{sir}. \\ $$
Commented by I want to learn more last updated on 22/May/20
But i got the question from the auxilliary equations
$$\mathrm{But}\:\mathrm{i}\:\mathrm{got}\:\mathrm{the}\:\mathrm{question}\:\mathrm{from}\:\mathrm{the}\:\mathrm{auxilliary}\:\mathrm{equations} \\ $$
Commented by prakash jain last updated on 22/May/20
You may want to just do a internet search on “recurrence relation”. You will find some general techinques on how to solve recurrence relation. Sometime you have to do a variable subtituion to convert to linear recurrence (ex. Q93173)
$$\mathrm{You}\:\mathrm{may}\:\mathrm{want}\:\mathrm{to}\:\mathrm{just}\:\mathrm{do}\:\mathrm{a}\:\mathrm{internet} \\ $$$$\mathrm{search}\:\mathrm{on}\:“\mathrm{recurrence}\:\mathrm{relation}''. \\ $$$$\mathrm{You}\:\mathrm{will}\:\mathrm{find}\:\mathrm{some}\:\mathrm{general}\:\mathrm{techinques} \\ $$$$\mathrm{on}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{recurrence}\:\mathrm{relation}. \\ $$$$\mathrm{Sometime}\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{do}\:\mathrm{a}\:\mathrm{variable} \\ $$$$\mathrm{subtituion}\:\mathrm{to}\:\mathrm{convert}\:\mathrm{to}\:\mathrm{linear} \\ $$$$\mathrm{recurrence}\:\left(\mathrm{ex}.\:\mathrm{Q93173}\right) \\ $$
Commented by I want to learn more last updated on 22/May/20
I can express negative base like y_(n − 2) + y_(n − 1) but i cannot find aucilliary of y_(n + 2) + y_(n + 3) + ... for positive base and negative together.
$$\mathrm{I}\:\mathrm{can}\:\mathrm{express}\:\mathrm{negative}\:\mathrm{base}\:\mathrm{like} \\ $$$$\:\:\:\mathrm{y}_{\mathrm{n}\:−\:\mathrm{2}} \:+\:\mathrm{y}_{\mathrm{n}\:−\:\mathrm{1}} \\ $$$$\mathrm{but}\:\mathrm{i}\:\mathrm{cannot}\:\mathrm{find}\:\mathrm{aucilliary}\:\mathrm{of} \\ $$$$\:\:\:\:\:\:\mathrm{y}_{\mathrm{n}\:+\:\mathrm{2}} \:\:+\:\:\mathrm{y}_{\mathrm{n}\:\:+\:\:\mathrm{3}} \:+\:…\:\mathrm{for}\:\mathrm{positive}\:\mathrm{base}\:\mathrm{and}\:\mathrm{negative}\:\mathrm{together}. \\ $$
Commented by prakash jain last updated on 22/May/20
What matter is a difference say for example y_(n+2) =5y_n +3y_(n+1) Subtitue n=n−2 y_n =5y_(n−2) +3y_(n−1)
$$\mathrm{What}\:\mathrm{matter}\:\mathrm{is}\:\mathrm{a}\:\mathrm{difference}\:\mathrm{say} \\ $$$$\mathrm{for}\:\mathrm{example} \\ $$$${y}_{{n}+\mathrm{2}} =\mathrm{5}{y}_{{n}} +\mathrm{3}{y}_{{n}+\mathrm{1}} \\ $$$$\mathrm{Subtitue}\:{n}={n}−\mathrm{2} \\ $$$${y}_{{n}} =\mathrm{5}{y}_{{n}−\mathrm{2}} +\mathrm{3}{y}_{{n}−\mathrm{1}} \\ $$
Commented by I want to learn more last updated on 22/May/20
I appreciate. now i have an idea. Thanks for your time.
$$\:\mathrm{I}\:\mathrm{appreciate}.\:\mathrm{now}\:\mathrm{i}\:\mathrm{have}\:\mathrm{an}\:\mathrm{idea}. \\ $$$$\mathrm{Thanks}\:\mathrm{for}\:\mathrm{your}\:\mathrm{time}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *