Question Number 35244 by JOHNMASANJA last updated on 17/May/18
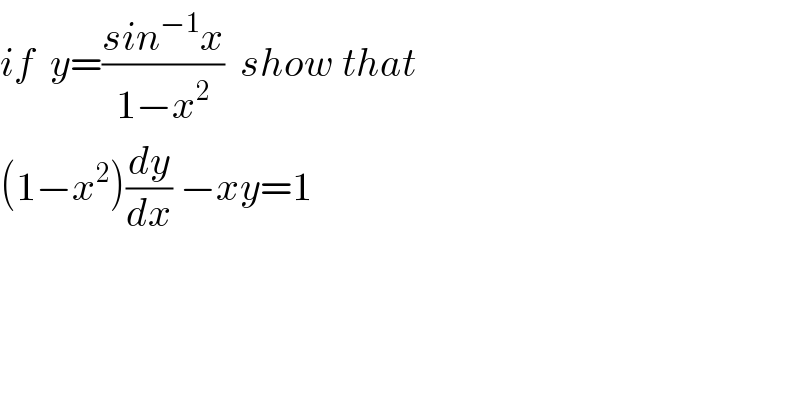
$${if}\:\:{y}=\frac{{sin}^{−\mathrm{1}} {x}}{\mathrm{1}−{x}^{\mathrm{2}} }\:\:{show}\:{that}\: \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}\:−{xy}=\mathrm{1} \\ $$
Commented by math1967 last updated on 17/May/18

$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){y}=\mathrm{sin}^{−\mathrm{1}} {x} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}−\mathrm{2}{xy}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \frac{{dy}}{{dx}}\:−\mathrm{2}{xy}=\mathrm{1} \\ $$$${But}\:{not}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}\:−\mathrm{2}{xy}=\mathrm{1} \\ $$$$????????????? \\ $$
