Question Number 45413 by mondodotto@gmail.com last updated on 12/Oct/18
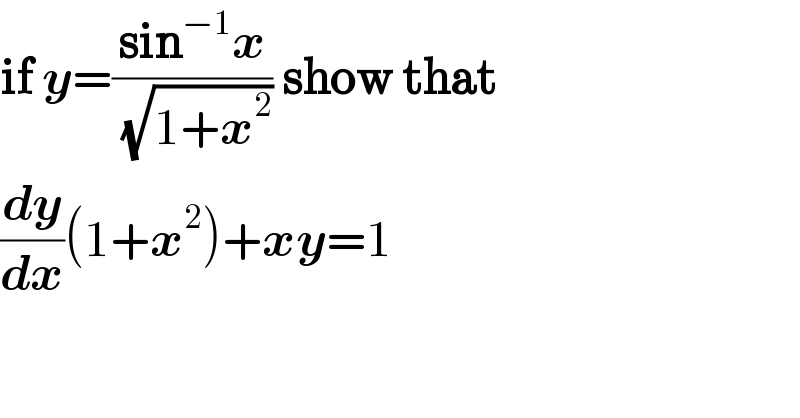
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{{y}}=\frac{\boldsymbol{\mathrm{sin}}^{−\mathrm{1}} \boldsymbol{{x}}}{\:\sqrt{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }}\:\boldsymbol{\mathrm{show}}\:\boldsymbol{\mathrm{that}} \\ $$$$\frac{\boldsymbol{{dy}}}{\boldsymbol{{dx}}}\left(\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} \right)+\boldsymbol{{xy}}=\mathrm{1} \\ $$
Commented by maxmathsup by imad last updated on 13/Oct/18

$${we}\:{have}\:{y}\left({x}\right)=\frac{{arcsinx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\Rightarrow{y}\left({x}\right)\:=\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {acsinx}\:\Rightarrow \\ $$$${y}^{'} \left({x}\right)\:=−{x}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{arcsinx}\:+\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{2}} \right){y}^{'} \left({x}\right)\:+{xy}\:=−{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{arcsinx}\:+\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:+\:{x}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:{arcsinx} \\ $$$$=\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:\:\:\:{finally}\:{thre}\:{is}\:{a}\:{error}\:{at}\:{the}\:{question}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18

$$\frac{{dy}}{{dx}}+\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{y}=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${intregaying}\:{factor} \\ $$$${e}^{\int\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}} \\ $$$${e}^{\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{d}\left(\mathrm{1}+{x}^{\mathrm{3}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${e}^{\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)} \\ $$$${e}^{{ln}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)} =\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\: \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\frac{{dy}}{{dx}}+{x}.\frac{{y}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\: \\ $$$$\frac{{d}}{{dx}}\left(\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:×{y}\right)=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\: \\ $$$${d}\left({y}×\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$$\int{d}\left({y}×\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)=\int\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx} \\ $$$${y}×\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:=\frac{{x}}{\mathrm{2}}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\left.\right)^{\mathrm{2}} } }\:\right. \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18

$${check}\:{the}\:{question}… \\ $$
Commented by mondodotto@gmail.com last updated on 12/Oct/18

$$\mathrm{sir}\:\mathrm{we}\:\mathrm{need}\:\mathrm{to}\:\mathrm{prove} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18
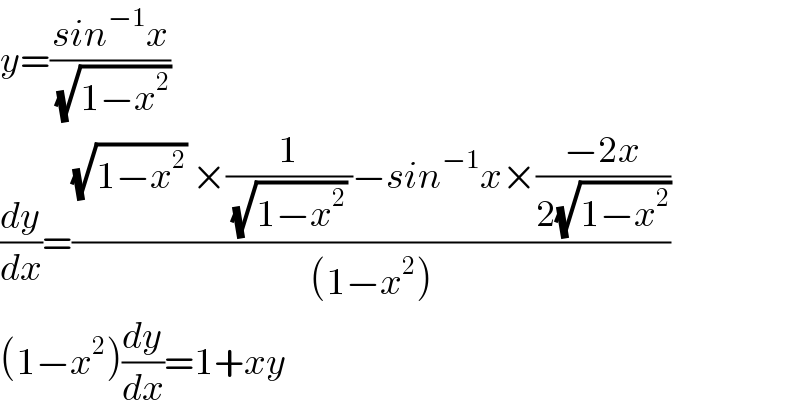
$${y}=\frac{{sin}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\frac{{dy}}{{dx}}=\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:}−{sin}^{−\mathrm{1}} {x}×\frac{−\mathrm{2}{x}}{\mathrm{2}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)} \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\frac{{dy}}{{dx}}=\mathrm{1}+{xy} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 12/Oct/18

$${pls}\:{check}… \\ $$
Commented by mondodotto@gmail.com last updated on 12/Oct/18

$$\mathrm{oky}\:\mathrm{sir} \\ $$
