Question Number 28305 by NECx last updated on 23/Jan/18
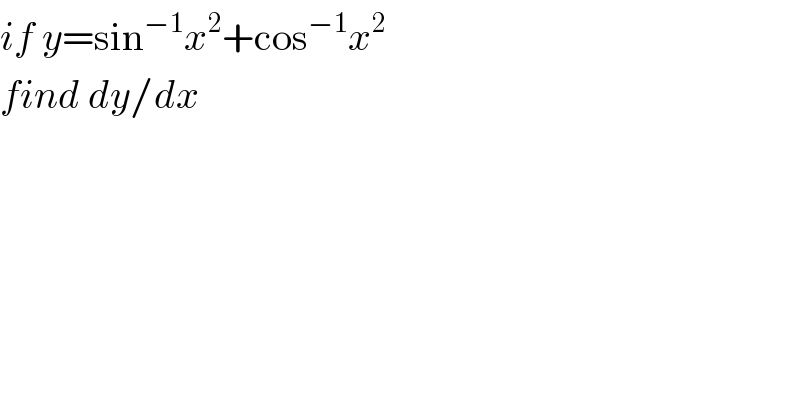
$${if}\:{y}=\mathrm{sin}^{−\mathrm{1}} {x}^{\mathrm{2}} +\mathrm{cos}^{−\mathrm{1}} {x}^{\mathrm{2}} \\ $$$${find}\:{dy}/{dx} \\ $$
Commented by abdo imad last updated on 23/Jan/18
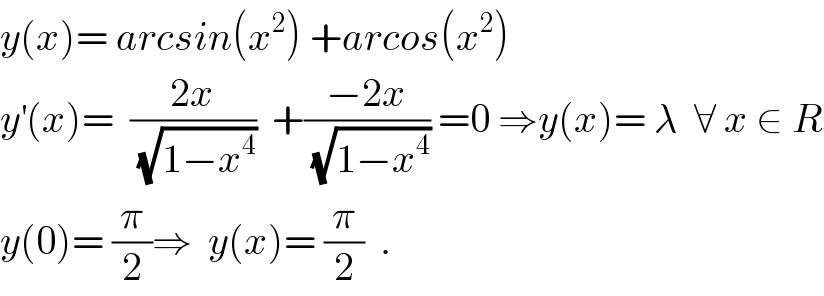
$${y}\left({x}\right)=\:{arcsin}\left({x}^{\mathrm{2}} \right)\:+{arcos}\left({x}^{\mathrm{2}} \right) \\ $$$${y}^{'} \left({x}\right)=\:\:\frac{\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:\:+\frac{−\mathrm{2}{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:=\mathrm{0}\:\Rightarrow{y}\left({x}\right)=\:\lambda\:\:\forall\:{x}\:\in\:{R} \\ $$$${y}\left(\mathrm{0}\right)=\:\frac{\pi}{\mathrm{2}}\Rightarrow\:\:{y}\left({x}\right)=\:\frac{\pi}{\mathrm{2}}\:\:. \\ $$
Commented by abdo imad last updated on 23/Jan/18
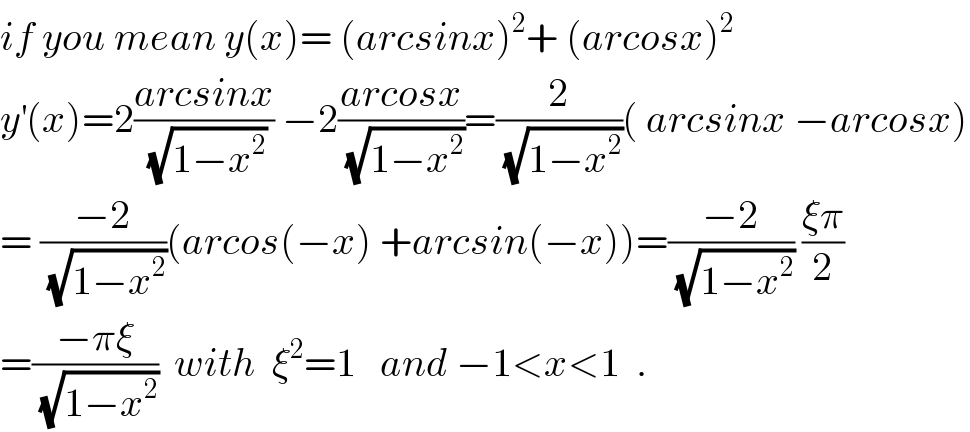
$${if}\:{you}\:{mean}\:{y}\left({x}\right)=\:\left({arcsinx}\right)^{\mathrm{2}} +\:\left({arcosx}\right)^{\mathrm{2}} \\ $$$${y}^{'} \left({x}\right)=\mathrm{2}\frac{{arcsinx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:−\mathrm{2}\frac{{arcosx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left(\:{arcsinx}\:−{arcosx}\right) \\ $$$$=\:\frac{−\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left({arcos}\left(−{x}\right)\:+{arcsin}\left(−{x}\right)\right)=\frac{−\mathrm{2}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\frac{\xi\pi}{\mathrm{2}} \\ $$$$=\frac{−\pi\xi}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:\:{with}\:\:\xi^{\mathrm{2}} =\mathrm{1}\:\:\:{and}\:−\mathrm{1}<{x}<\mathrm{1}\:\:. \\ $$
Commented by NECx last updated on 24/Jan/18
$${thank}\:{you}\:{so}\:{much}. \\ $$
