Question Number 33407 by NECx last updated on 15/Apr/18
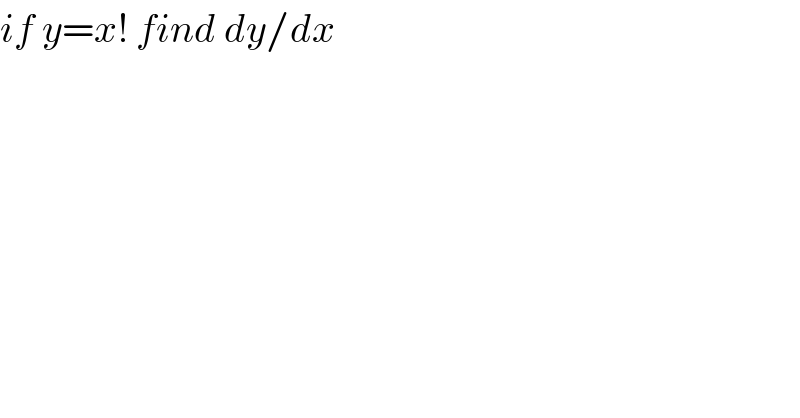
$${if}\:{y}={x}!\:{find}\:{dy}/{dx} \\ $$
Answered by MJS last updated on 15/Apr/18
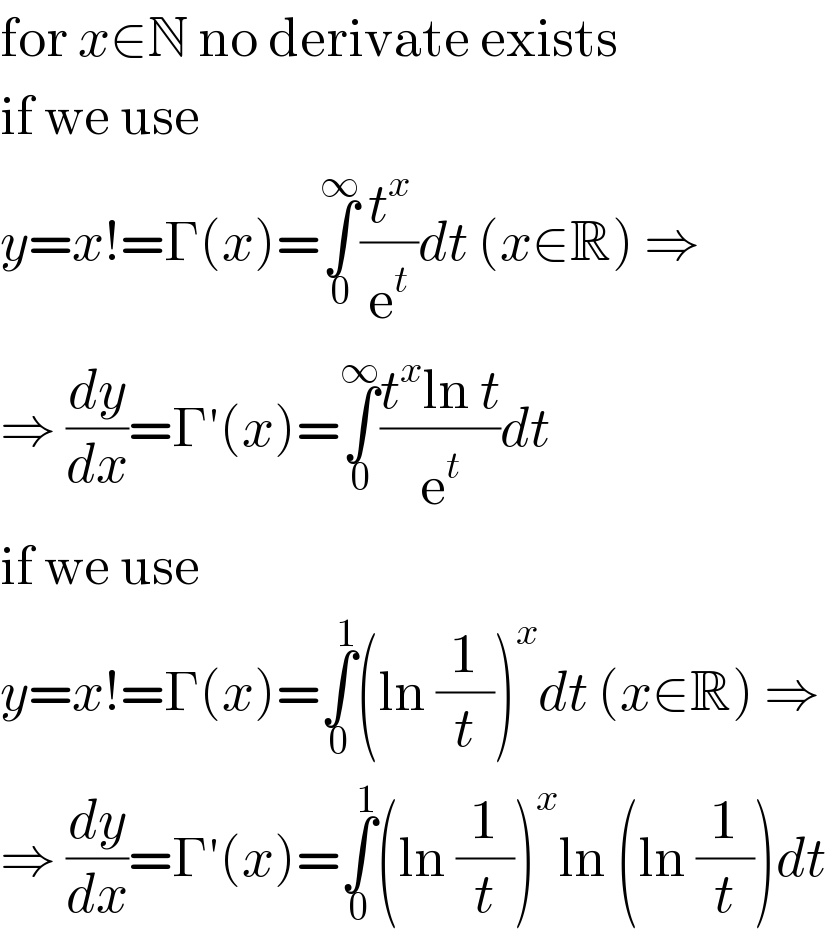
$$\mathrm{for}\:{x}\in\mathbb{N}\:\mathrm{no}\:\mathrm{derivate}\:\mathrm{exists} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{use} \\ $$$${y}={x}!=\Gamma\left({x}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{{x}} }{\mathrm{e}^{{t}} }{dt}\:\left({x}\in\mathbb{R}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=\Gamma'\left({x}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{t}^{{x}} \mathrm{ln}\:{t}}{\mathrm{e}^{{t}} }{dt} \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{use} \\ $$$${y}={x}!=\Gamma\left({x}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{ln}\:\frac{\mathrm{1}}{{t}}\right)^{{x}} {dt}\:\left({x}\in\mathbb{R}\right)\:\Rightarrow \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=\Gamma'\left({x}\right)=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{ln}\:\frac{\mathrm{1}}{{t}}\right)^{{x}} \mathrm{ln}\:\left(\mathrm{ln}\:\frac{\mathrm{1}}{{t}}\right){dt} \\ $$
Commented by prof Abdo imad last updated on 15/Apr/18
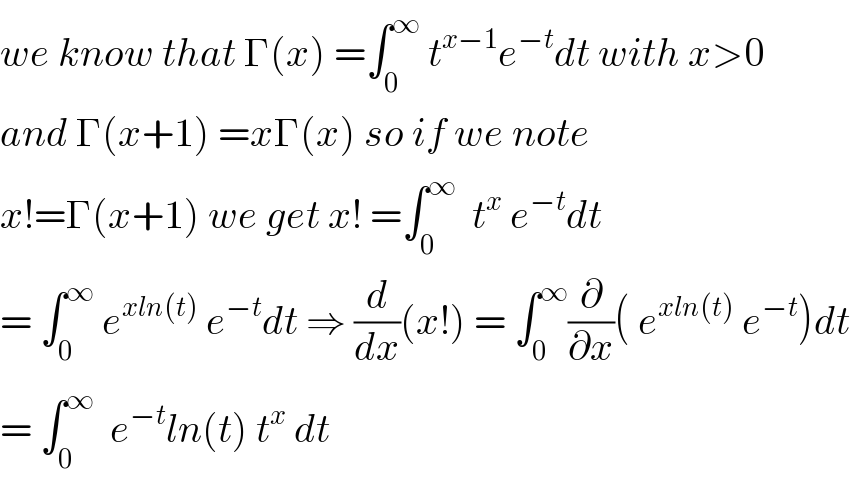
$${we}\:{know}\:{that}\:\Gamma\left({x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} {e}^{−{t}} {dt}\:{with}\:{x}>\mathrm{0} \\ $$$${and}\:\Gamma\left({x}+\mathrm{1}\right)\:={x}\Gamma\left({x}\right)\:{so}\:{if}\:{we}\:{note} \\ $$$${x}!=\Gamma\left({x}+\mathrm{1}\right)\:{we}\:{get}\:{x}!\:=\int_{\mathrm{0}} ^{\infty} \:\:{t}^{{x}} \:{e}^{−{t}} {dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:{e}^{{xln}\left({t}\right)} \:{e}^{−{t}} {dt}\:\Rightarrow\:\frac{{d}}{{dx}}\left({x}!\right)\:=\:\int_{\mathrm{0}} ^{\infty} \frac{\partial}{\partial{x}}\left(\:{e}^{{xln}\left({t}\right)} \:{e}^{−{t}} \right){dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−{t}} {ln}\left({t}\right)\:{t}^{{x}} \:{dt}\: \\ $$
