Question Number 175937 by qaz last updated on 09/Sep/22
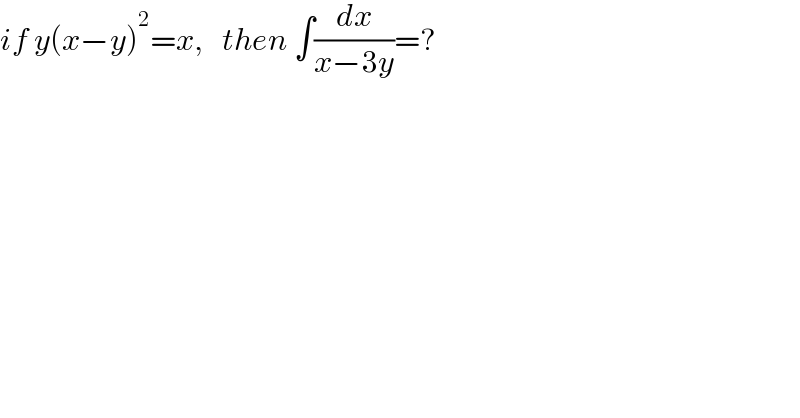
$${if}\:{y}\left({x}−{y}\right)^{\mathrm{2}} ={x},\:\:\:{then}\:\int\frac{{dx}}{{x}−\mathrm{3}{y}}=? \\ $$
Answered by Frix last updated on 11/Sep/22
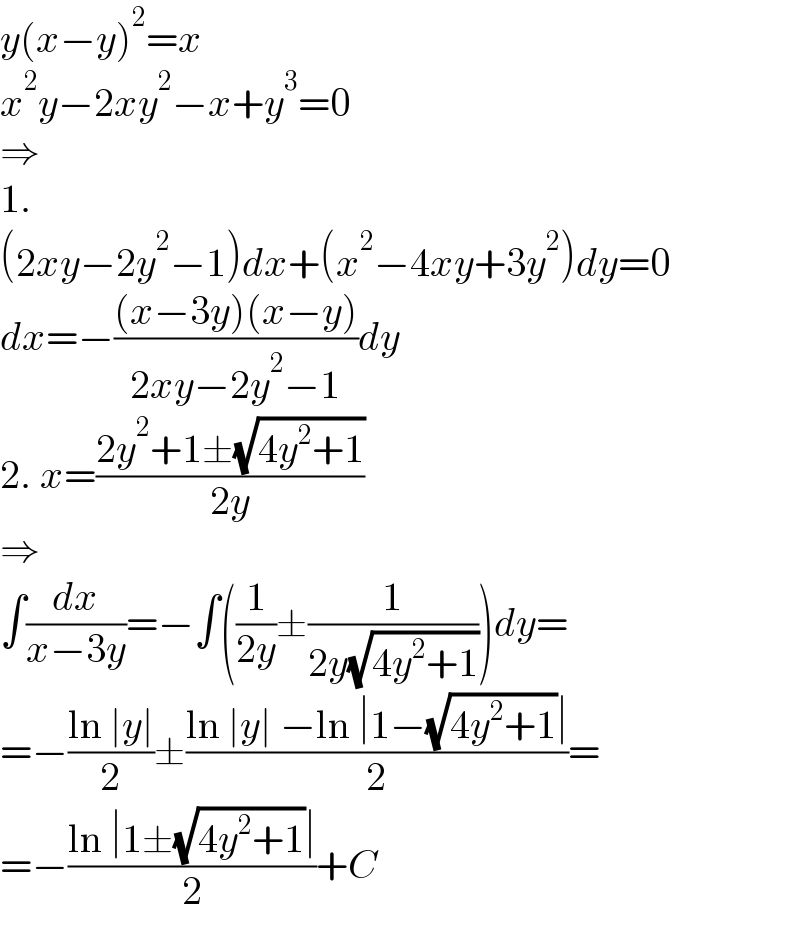
$${y}\left({x}−{y}\right)^{\mathrm{2}} ={x} \\ $$$${x}^{\mathrm{2}} {y}−\mathrm{2}{xy}^{\mathrm{2}} −{x}+{y}^{\mathrm{3}} =\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\mathrm{1}. \\ $$$$\left(\mathrm{2}{xy}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}\right){dx}+\left({x}^{\mathrm{2}} −\mathrm{4}{xy}+\mathrm{3}{y}^{\mathrm{2}} \right){dy}=\mathrm{0} \\ $$$${dx}=−\frac{\left({x}−\mathrm{3}{y}\right)\left({x}−{y}\right)}{\mathrm{2}{xy}−\mathrm{2}{y}^{\mathrm{2}} −\mathrm{1}}{dy} \\ $$$$\mathrm{2}.\:{x}=\frac{\mathrm{2}{y}^{\mathrm{2}} +\mathrm{1}\pm\sqrt{\mathrm{4}{y}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}{y}} \\ $$$$\Rightarrow \\ $$$$\int\frac{{dx}}{{x}−\mathrm{3}{y}}=−\int\left(\frac{\mathrm{1}}{\mathrm{2}{y}}\pm\frac{\mathrm{1}}{\mathrm{2}{y}\sqrt{\mathrm{4}{y}^{\mathrm{2}} +\mathrm{1}}}\right){dy}= \\ $$$$=−\frac{\mathrm{ln}\:\mid{y}\mid}{\mathrm{2}}\pm\frac{\mathrm{ln}\:\mid{y}\mid\:−\mathrm{ln}\:\mid\mathrm{1}−\sqrt{\mathrm{4}{y}^{\mathrm{2}} +\mathrm{1}}\mid}{\mathrm{2}}= \\ $$$$=−\frac{\mathrm{ln}\:\mid\mathrm{1}\pm\sqrt{\mathrm{4}{y}^{\mathrm{2}} +\mathrm{1}}\mid}{\mathrm{2}}+{C} \\ $$
