Menu Close

if-y-xtan-1-x-1-2-ln-1-x-2-show-that-1-x-2-y-1-

Tinku Tara 0 Comments
Pin




Question Number 20872 by j.masanja06@gmail.com last updated on 05/Sep/17
if y=[xtan^(−1) x]−[(1/2)ln(1+x^2 )] show that (1+x^2 )y^(′′) =1
ify=[xtan−1x]−[12ln(1+x2)]showthat(1+x2)y″=1
Answered by sma3l2996 last updated on 05/Sep/17
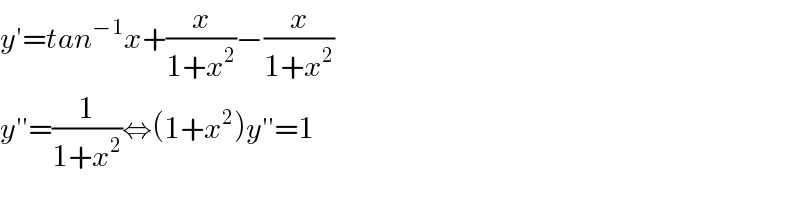
y′=tan^(−1) x+(x/(1+x^2 ))−(x/(1+x^2 )) y′′=(1/(1+x^2 ))⇔(1+x^2 )y′′=1
y′=tan−1x+x1+x2−x1+x2y″=11+x2⇔(1+x2)y″=1

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *