Question Number 109396 by ZiYangLee last updated on 23/Aug/20
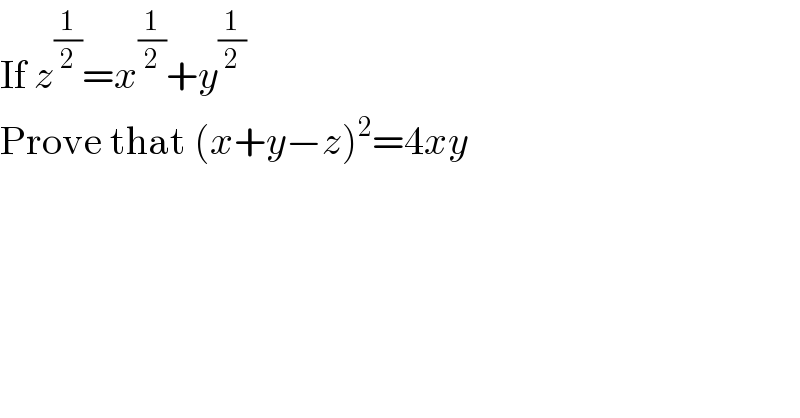
$$\mathrm{If}\:{z}^{\frac{\mathrm{1}}{\mathrm{2}}} ={x}^{\frac{\mathrm{1}}{\mathrm{2}}} +{y}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{Prove}\:\mathrm{that}\:\left({x}+{y}−{z}\right)^{\mathrm{2}} =\mathrm{4}{xy} \\ $$
Answered by bemath last updated on 23/Aug/20
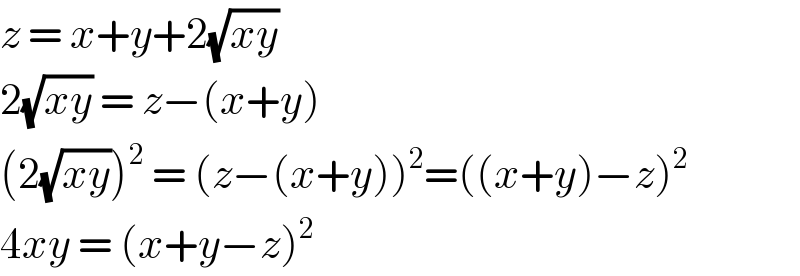
$${z}\:=\:{x}+{y}+\mathrm{2}\sqrt{{xy}}\: \\ $$$$\mathrm{2}\sqrt{{xy}}\:=\:{z}−\left({x}+{y}\right) \\ $$$$\left(\mathrm{2}\sqrt{{xy}}\right)^{\mathrm{2}} \:=\:\left({z}−\left({x}+{y}\right)\right)^{\mathrm{2}} =\left(\left({x}+{y}\right)−{z}\right)^{\mathrm{2}} \\ $$$$\mathrm{4}{xy}\:=\:\left({x}+{y}−{z}\right)^{\mathrm{2}} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Aug/20

$$\in×\subset\in\mid\mid\in\cap\top! \\ $$
Commented by ZiYangLee last updated on 23/Aug/20

$$\mathrm{Yay}! \\ $$
