Menu Close

If-z-1-2-z-2-3-z-3-4-and-2z-1-3z-2-4z-3-4-then-the-expression-8z-2-z-3-27z-3-z-1-64z-1-z-2-equals-

Tinku Tara 0 Comments
Pin




Question Number 20739 by Tinkutara last updated on 02/Sep/17
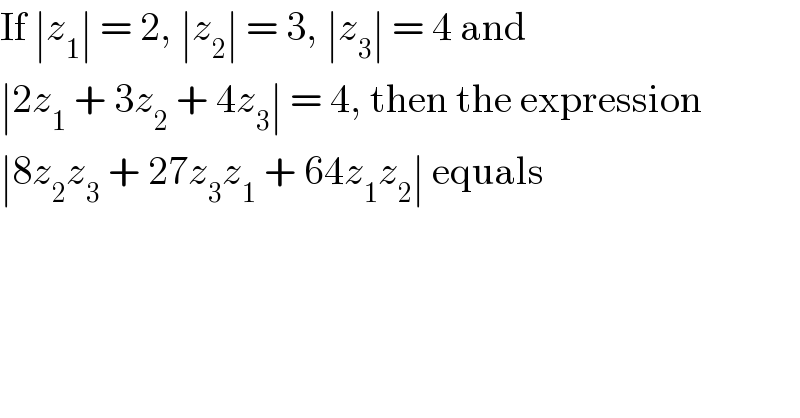
If ∣z_1 ∣ = 2, ∣z_2 ∣ = 3, ∣z_3 ∣ = 4 and ∣2z_1 + 3z_2 + 4z_3 ∣ = 4, then the expression ∣8z_2 z_3 + 27z_3 z_1 + 64z_1 z_2 ∣ equals
$$\mathrm{If}\:\mid{z}_{\mathrm{1}} \mid\:=\:\mathrm{2},\:\mid{z}_{\mathrm{2}} \mid\:=\:\mathrm{3},\:\mid{z}_{\mathrm{3}} \mid\:=\:\mathrm{4}\:\mathrm{and} \\ $$$$\mid\mathrm{2}{z}_{\mathrm{1}} \:+\:\mathrm{3}{z}_{\mathrm{2}} \:+\:\mathrm{4}{z}_{\mathrm{3}} \mid\:=\:\mathrm{4},\:\mathrm{then}\:\mathrm{the}\:\mathrm{expression} \\ $$$$\mid\mathrm{8}{z}_{\mathrm{2}} {z}_{\mathrm{3}} \:+\:\mathrm{27}{z}_{\mathrm{3}} {z}_{\mathrm{1}} \:+\:\mathrm{64}{z}_{\mathrm{1}} {z}_{\mathrm{2}} \mid\:\mathrm{equals} \\ $$
Answered by $@ty@m last updated on 02/Sep/17
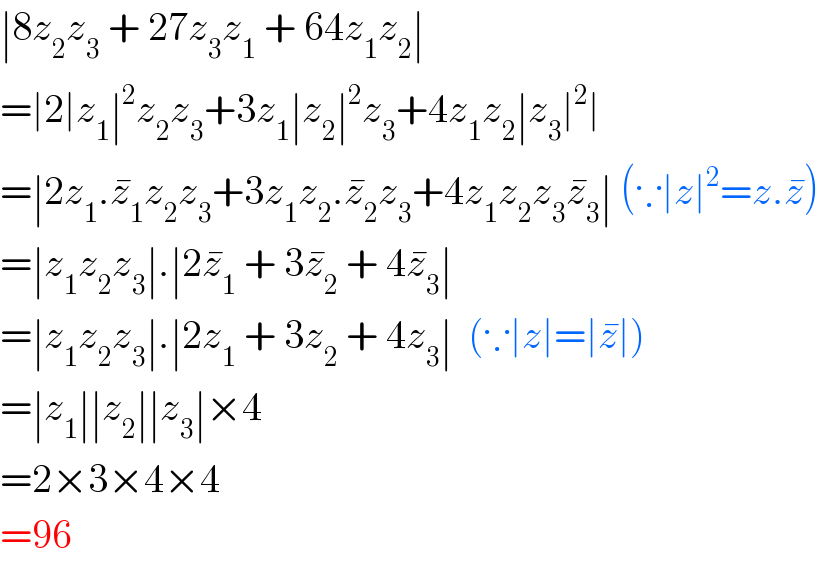
∣8z_2 z_3 + 27z_3 z_1 + 64z_1 z_2 ∣ =∣2∣z_1 ∣^2 z_2 z_3 +3z_1 ∣z_2 ∣^2 z_3 +4z_1 z_2 ∣z_3 ∣^2 ∣ =∣2z_1 .z_1 ^� z_2 z_3 +3z_1 z_2 .z_2 ^� z_3 +4z_1 z_2 z_3 z_3 ^� ∣ (∵∣z∣^2 =z.z^� ) =∣z_1 z_2 z_3 ∣.∣2z_1 ^� + 3z_2 ^� + 4z_3 ^� ∣ =∣z_1 z_2 z_3 ∣.∣2z_1 + 3z_2 + 4z_3 ∣ (∵∣z∣=∣z^� ∣) =∣z_1 ∣∣z_2 ∣∣z_3 ∣×4 =2×3×4×4 =96
$$\mid\mathrm{8}{z}_{\mathrm{2}} {z}_{\mathrm{3}} \:+\:\mathrm{27}{z}_{\mathrm{3}} {z}_{\mathrm{1}} \:+\:\mathrm{64}{z}_{\mathrm{1}} {z}_{\mathrm{2}} \mid\: \\ $$$$=\mid\mathrm{2}\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} +\mathrm{3}{z}_{\mathrm{1}} \mid{z}_{\mathrm{2}} \mid^{\mathrm{2}} {z}_{\mathrm{3}} +\mathrm{4}{z}_{\mathrm{1}} {z}_{\mathrm{2}} \mid{z}_{\mathrm{3}} \mid^{\mathrm{2}} \mid \\ $$$$=\mid\mathrm{2}{z}_{\mathrm{1}} .\bar {{z}}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} +\mathrm{3}{z}_{\mathrm{1}} {z}_{\mathrm{2}} .\bar {{z}}_{\mathrm{2}} {z}_{\mathrm{3}} +\mathrm{4}{z}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} \bar {{z}}_{\mathrm{3}} \mid\:\left(\because\mid{z}\mid^{\mathrm{2}} ={z}.\bar {{z}}\right) \\ $$$$=\mid{z}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} \mid.\mid\mathrm{2}\bar {{z}}_{\mathrm{1}} \:+\:\mathrm{3}\bar {{z}}_{\mathrm{2}} \:+\:\mathrm{4}\bar {{z}}_{\mathrm{3}} \mid\: \\ $$$$=\mid{z}_{\mathrm{1}} {z}_{\mathrm{2}} {z}_{\mathrm{3}} \mid.\mid\mathrm{2}{z}_{\mathrm{1}} \:+\:\mathrm{3}{z}_{\mathrm{2}} \:+\:\mathrm{4}{z}_{\mathrm{3}} \mid\:\:\left(\because\mid{z}\mid=\mid\bar {{z}}\mid\right) \\ $$$$=\mid{z}_{\mathrm{1}} \mid\mid{z}_{\mathrm{2}} \mid\mid{z}_{\mathrm{3}} \mid×\mathrm{4}\:\: \\ $$$$=\mathrm{2}×\mathrm{3}×\mathrm{4}×\mathrm{4} \\ $$$$=\mathrm{96} \\ $$
Commented by Tinkutara last updated on 03/Sep/17
Thank you very much Sir!
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *