Question Number 19740 by Tinkutara last updated on 15/Aug/17
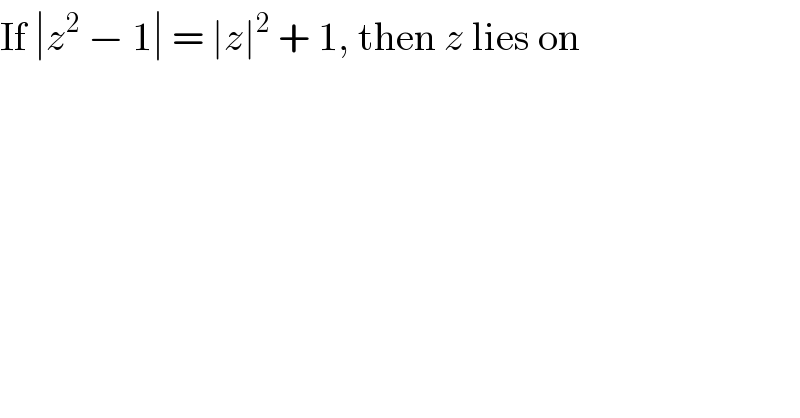
$$\mathrm{If}\:\mid{z}^{\mathrm{2}} \:−\:\mathrm{1}\mid\:=\:\mid{z}\mid^{\mathrm{2}} \:+\:\mathrm{1},\:\mathrm{then}\:{z}\:\mathrm{lies}\:\mathrm{on} \\ $$
Answered by ajfour last updated on 16/Aug/17
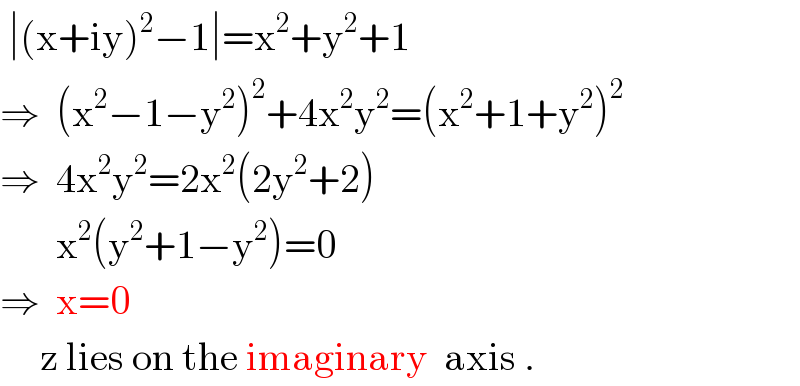
$$\:\mid\left(\mathrm{x}+\mathrm{iy}\right)^{\mathrm{2}} −\mathrm{1}\mid=\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{1} \\ $$$$\Rightarrow\:\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} =\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\mathrm{4x}^{\mathrm{2}} \mathrm{y}^{\mathrm{2}} =\mathrm{2x}^{\mathrm{2}} \left(\mathrm{2y}^{\mathrm{2}} +\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{x}^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} +\mathrm{1}−\mathrm{y}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{x}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{z}\:\mathrm{lies}\:\mathrm{on}\:\mathrm{the}\:\mathrm{imaginary}\:\:\mathrm{axis}\:. \\ $$
Commented by Tinkutara last updated on 15/Aug/17
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}! \\ $$
