if-z-27-find-all-the-root-of-z-in-complex-plain-

Question Number 36676 by tawa tawa last updated on 04/Jun/18

if z = - 27, find all the root of z in complex plain

Commented by abdo mathsup 649 cc last updated on 04/Jun/18

t h e r o o t s a r e ? t h e c o m l e x z / z^{2} = - 27 = {(i \sqrt{27})}^{2} s o

t h e r o o t s a r e i \sqrt{27} a n d - i \sqrt{27} .

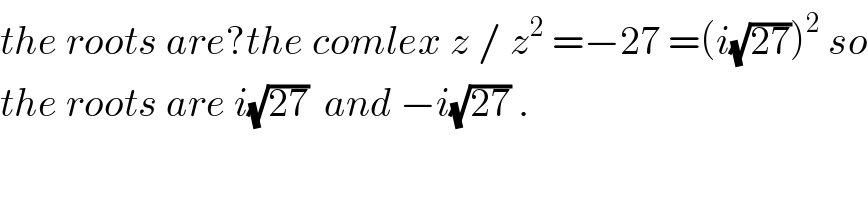
Commented by tawa tawa last updated on 04/Jun/18

God bless you sir .

Commented by abdo.msup.com last updated on 05/Jun/18

a l o t s o f t h a n k s s i r T a w a T a w a \dots

Answered by Rasheed.Sindhi last updated on 04/Jun/18

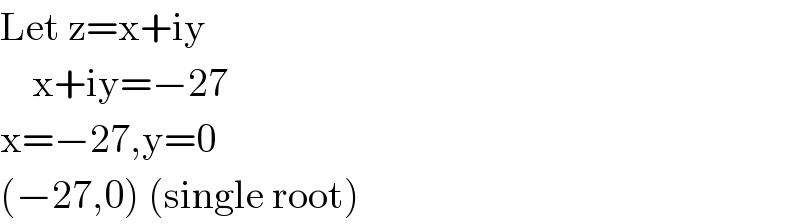
Let z = x + iy

x + iy = - 27

x = - 27, y = 0

(- 27, 0) (single root)

Commented by tawa tawa last updated on 05/Jun/18

God bless you sir