Question Number 125996 by bramlexs22 last updated on 16/Dec/20
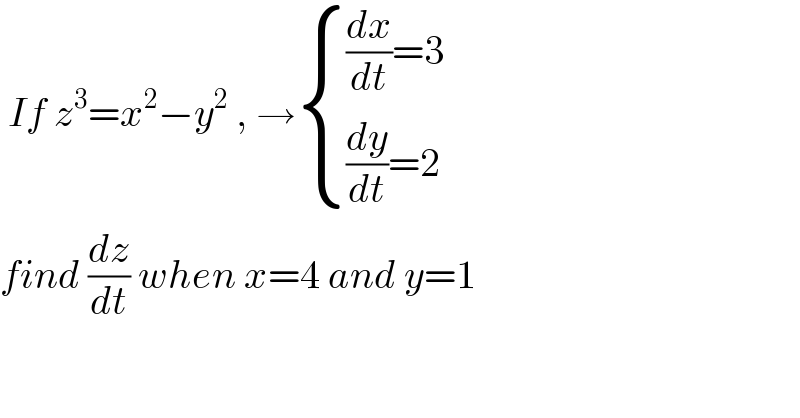
$$\:{If}\:{z}^{\mathrm{3}} ={x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:,\:\rightarrow\begin{cases}{\frac{{dx}}{{dt}}=\mathrm{3}}\\{\frac{{dy}}{{dt}}=\mathrm{2}}\end{cases} \\ $$$${find}\:\frac{{dz}}{{dt}}\:{when}\:{x}=\mathrm{4}\:{and}\:{y}=\mathrm{1} \\ $$
Answered by Olaf last updated on 16/Dec/20
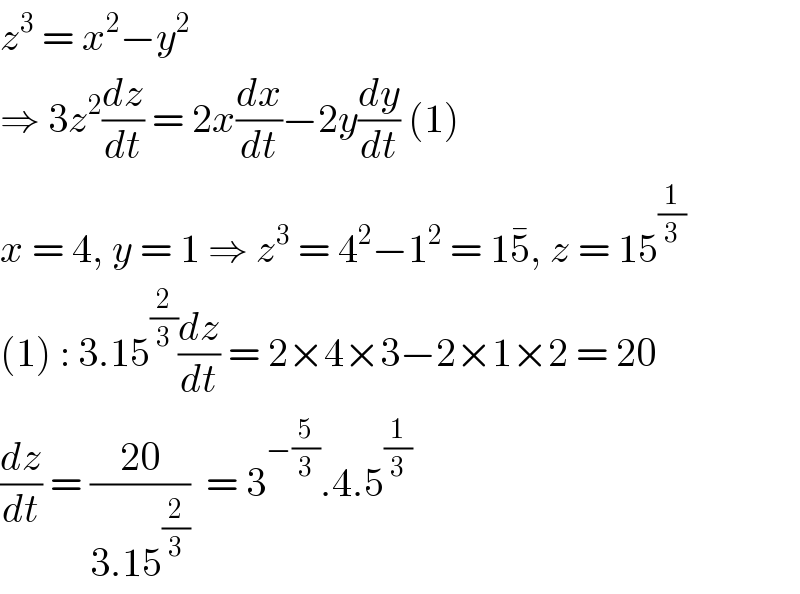
$${z}^{\mathrm{3}} \:=\:{x}^{\mathrm{2}} −{y}^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{3}{z}^{\mathrm{2}} \frac{{dz}}{{dt}}\:=\:\mathrm{2}{x}\frac{{dx}}{{dt}}−\mathrm{2}{y}\frac{{dy}}{{dt}}\:\left(\mathrm{1}\right) \\ $$$${x}\:=\:\mathrm{4},\:{y}\:=\:\mathrm{1}\:\Rightarrow\:{z}^{\mathrm{3}} \:=\:\mathrm{4}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} \:=\:\mathrm{1}\bar {\mathrm{5}},\:{z}\:=\:\mathrm{15}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\left(\mathrm{1}\right)\::\:\mathrm{3}.\mathrm{15}^{\frac{\mathrm{2}}{\mathrm{3}}} \frac{{dz}}{{dt}}\:=\:\mathrm{2}×\mathrm{4}×\mathrm{3}−\mathrm{2}×\mathrm{1}×\mathrm{2}\:=\:\mathrm{20} \\ $$$$\frac{{dz}}{{dt}}\:=\:\frac{\mathrm{20}}{\mathrm{3}.\mathrm{15}^{\frac{\mathrm{2}}{\mathrm{3}}} }\:\:=\:\mathrm{3}^{−\frac{\mathrm{5}}{\mathrm{3}}} .\mathrm{4}.\mathrm{5}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$
Commented by bramlexs22 last updated on 16/Dec/20

$${thanks} \\ $$
