If-z-6-8i-4-then-Minimum-value-of-z-is-A-4-B-5-C-6-D-8-

Question Number 32049 by rahul 19 last updated on 18/Mar/18

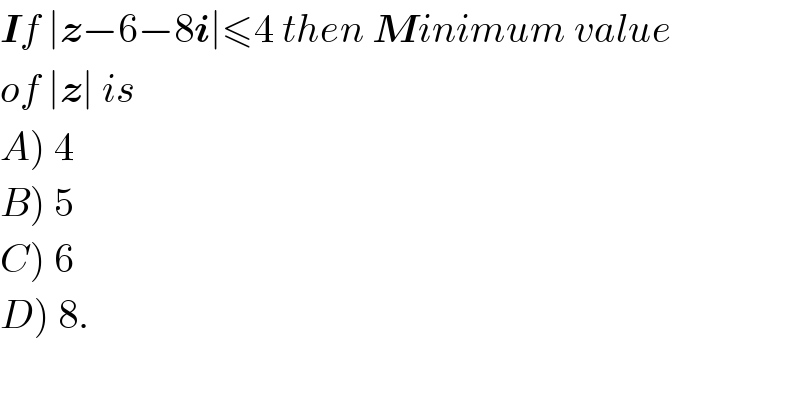
I f ∣ z - 6 - 8 i ∣⩽ 4 t h e n M i n i m u m v a l u e

o f ∣ z ∣ i s

A) 4

B) 5

C) 6

D) 8 .

Answered by mrW2 last updated on 18/Mar/18

\sqrt{6^{2} + 8^{2}} - 4 = 6

\Rightarrow a n s w e r C)

Commented by rahul 19 last updated on 18/Mar/18

t h a n k u s i r!

Answered by Tinkutara last updated on 18/Mar/18

Commented by Tinkutara last updated on 18/Mar/18

I n q u e s t i o n ∣ z - 6 - 8 i ∣⩽ 4

y o u w r o t e ∣ z - 6 - 8 i ∣⩽∣ z ∣ + ∣ - 6 - 8 i ∣

I n g e n e r a l a ⩽ b a n d a ⩽ c ⇏ b = c

e . g . 5 ⩽ 10 a n d 5 ⩽ 20 b u t 10 \neq 20

W e c a n n o t c o m p a r e b a n d c .

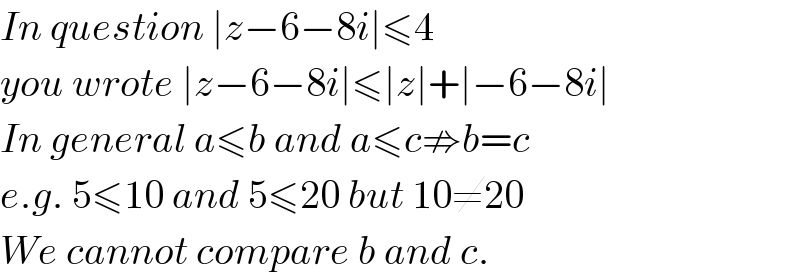
Commented by rahul 19 last updated on 18/Mar/18

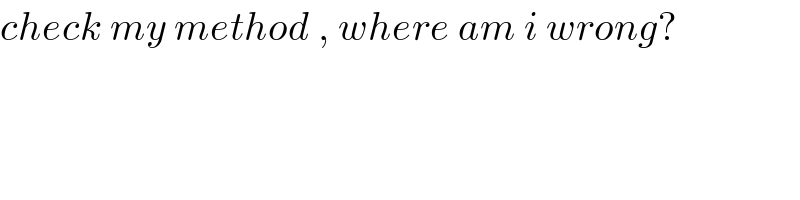
c h e c k m y m e t h o d, w h e r e a m i w r o n g ?

c h e c k m y m e t h o d, w h e r e a m i w r o n g ?

Commented by rahul 19 last updated on 18/Mar/18

o k, t h a n k s!

o k, t h a n k s!

Commented by Tinkutara last updated on 18/Mar/18

Locus of z is a circle and its inside. Hence calculating the minimum distance from origin.