If-z-cos-isin-is-a-root-of-equation-a-0-z-n-a-1-z-n-1-a-2-z-n-2-a-n-1-z-a-n-0-then-prove-that-i-a-0-a-1-cos-a-2-cos-2-a-n-cos-n-0-ii-a-1-sin-a-2-sin-2-a-n-sin

Question Number 32160 by rahul 19 last updated on 20/Mar/18

\boldsymbol I f z = c o s θ + i s i n θ i s a r o o t o f e q u a t i o n

a_{0} z^{n} + a_{1} z^{n - 1} + a_{2} z^{n - 2} + \dots . . + a_{n - 1} z + a_{n} = 0

t h e n p r o v e t h a t :

i) a_{0} + a_{1} \cos θ + a_{2} \cos 2 θ + \dots . . + a_{n} \cos n θ = 0

i i) a_{1} \sin θ + a_{2} \sin 2 θ + \dots . + a_{n} \sin n θ = 0 .

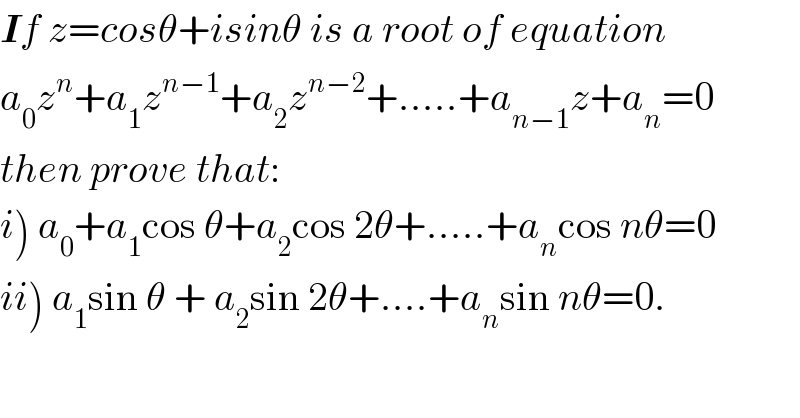
Answered by rahul 19 last updated on 20/Mar/18

M y t r y :

D i v i d i n g t h e w h o l e {e q}^{n} b y z^{n},

\Rightarrow a_{0} + a_{1} z^{- 1} + \dots \dots . + a_{n - 1} z^{1 - n} + a_{n} z^{- n} = 0

N o w z s a t i s f i e s t h e a b o v e {e q}^{n},

\Rightarrow a_{0} + a_{1} (\cos θ - i \sin θ) + \dots \dots \dots . .

\Rightarrow \dots + a_{n - 1} (c o s (n - 1) θ - i s i n (n - 1) θ)

\Rightarrow + a_{n} (c o s n θ - i s i n n θ) = 0 .

(b y d e {m o i v r e}^{'} s t h e o r e m) .

\boldsymbol C o l l e c t i n g t h e r e a l a n d i m a g i n a r y

p a r t s e p e r a t e l y,

\Rightarrow (a_{0} + a_{1} \cos θ + a_{2} \cos 2 θ + \dots . . + a_{n} \cos n θ)

- i (a_{1} \sin θ + a_{2} \sin 2 θ + \dots . . + a_{n} \sin n θ) = 0

H o w t o p r o c e e d f u r t h e r ?

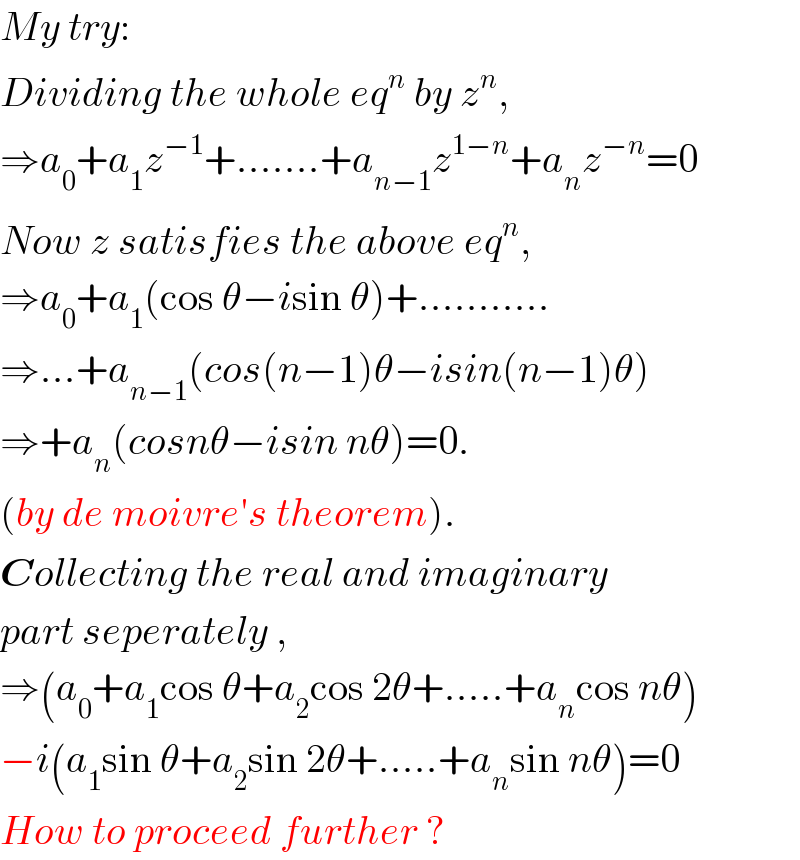
Commented by rahul 19 last updated on 21/Mar/18

h e y, @ a b o v e b u t h e r e m y n o . i s

a - i b = 0 \Rightarrow a = i b s o i s i t c o m p u l s o r y t h a t

a = b = 0 .

Commented by Tinkutara last updated on 20/Mar/18

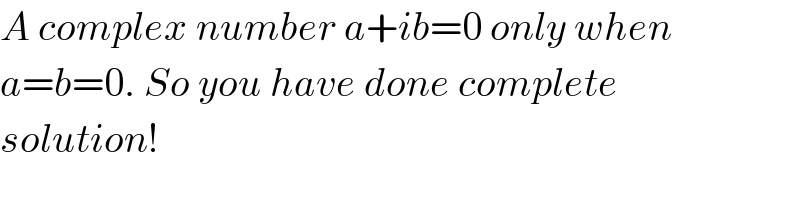
A c o m p l e x n u m b e r a + i b = 0 o n l y w h e n

a = b = 0 . S o y o u h a v e d o n e c o m p l e t e

s o l u t i o n!

Commented by rahul 19 last updated on 20/Mar/18

H a h a h a \dots . .

t h a n k s f o r c h e c k i n g!

Commented by mrW2 last updated on 21/Mar/18

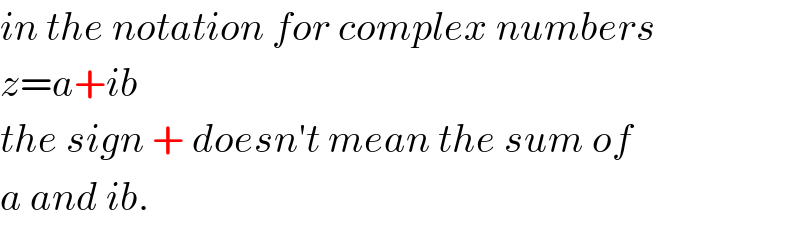
i n t h e n o t a t i o n f o r c o m p l e x n u m b e r s

z = a + i b

t h e s i g n + {d o e s n}^{'} t m e a n t h e s u m o f

a a n d i b .

Commented by mrW2 last updated on 21/Mar/18

Commented by rahul 19 last updated on 21/Mar/18

o k, t h a n k y o u s i r .

o k, t h a n k y o u s i r .