Menu Close

If-z-z-2-3x-3y-0-prove-that-2-z-x-2-2-z-y-2-2z-x-1-z-2-x-3-please-help-

Tinku Tara 0 Comments
Pin




Question Number 89178 by necxxx last updated on 15/Apr/20
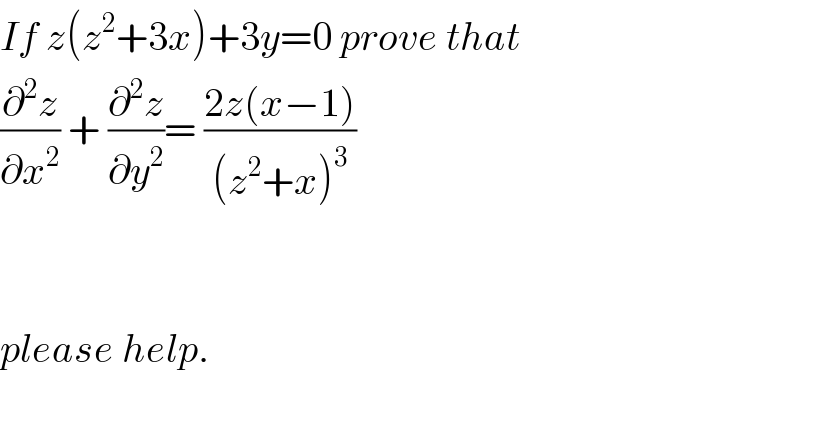
If z(z^2 +3x)+3y=0 prove that (∂^2 z/∂x^2 ) + (∂^2 z/∂y^2 )= ((2z(x−1))/((z^2 +x)^3 )) please help.
$${If}\:{z}\left({z}^{\mathrm{2}} +\mathrm{3}{x}\right)+\mathrm{3}{y}=\mathrm{0}\:{prove}\:{that}\: \\ $$$$\frac{\partial^{\mathrm{2}} {z}}{\partial{x}^{\mathrm{2}} }\:+\:\frac{\partial^{\mathrm{2}} {z}}{\partial{y}^{\mathrm{2}} }=\:\frac{\mathrm{2}{z}\left({x}−\mathrm{1}\right)}{\left({z}^{\mathrm{2}} +{x}\right)^{\mathrm{3}} } \\ $$$$ \\ $$$$ \\ $$$${please}\:{help}. \\ $$$$ \\ $$
Commented by niroj last updated on 16/Apr/20
If z(z^2 +3x)+3y=0 Prove that (∂^2 z/∂x^2 ) +(∂^2 z/∂y^2 ) = ((2z(x−1))/((z^2 +x)^3 )) D.w.r.to x z^3 +3xz +3y=0 3z^2 .(dz/dx)+3z+3x(dz/dx)=0 3 (dz/dx)(z^2 +x)=−3z (dz/dx)= ((−z)/(z^2 +x))= (d^2 z/dx^2 )= ((−(dz/dx)(z^2 +x)+z(2z.(dz/dx)+1))/((z^2 +x)^2 )) = ((−(dz/dx)(z^2 +x)+2z^2 (dz/dx)+z)/((z^2 +x)^2 )) = (((dz/dx)(2z^2 −z^2 −x)+z)/((z^2 +x)^2 ))= ((((−z)/(z^2 +x))(z^2 −x)+z)/((z^2 +x)^2 )) = ((xz−z^3 +z^3 +zx)/((z^2 +x)^3 ))= ((2zx)/((z^2 +x)^3 )) Again, D.w.r.to.y z^3 +3xz+3y=0 3z^2 (dz/dy)+3x(dz/dy)+3=0 3(dz/dy)(z^2 +x)=−3 (dz/dy)= −1.(z^2 +x)^(−1) (d^2 z/dy^2 )= −1.(−1)(z^2 +x)^(−2) .2z(dz/dy) = ((2z)/((z^2 +x)^2 )).((−1)/((z^2 +x))) = ((−2z)/((z^2 +x)^3 )) now, (∂^2 z/∂x^2 )+(∂^2 z/∂^2 y)= ((2xz)/((z^2 +x)^3 ))+((−2z)/((z^2 +x)^3 )) = ((2xz−2z)/((z^2 +x)^3 ))= ((2z(x−1))/((z^2 +x)^3 )) hence ∴ (∂^2 z/∂x^2 )+ (∂^2 z/∂y^2 )= ((2z(x−1))/((z^2 +x)^3 )) Proved//.
$$\:\:\:\boldsymbol{\mathrm{If}}\:\:\boldsymbol{\mathrm{z}}\left(\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\mathrm{3}\boldsymbol{\mathrm{x}}\right)+\mathrm{3}\boldsymbol{\mathrm{y}}=\mathrm{0}\:\boldsymbol{\mathrm{P}}\mathrm{rove}\:\mathrm{that}\: \\ $$$$\:\:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{x}^{\mathrm{2}} }\:+\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{y}^{\mathrm{2}} }\:=\:\frac{\mathrm{2z}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$\:\mathrm{D}.\mathrm{w}.\mathrm{r}.\mathrm{to}\:\mathrm{x} \\ $$$$\:\:\:\:\mathrm{z}^{\mathrm{3}} +\mathrm{3xz}\:+\mathrm{3y}=\mathrm{0} \\ $$$$\:\:\:\:\mathrm{3z}^{\mathrm{2}} .\frac{\mathrm{dz}}{\mathrm{dx}}+\mathrm{3z}+\mathrm{3x}\frac{\mathrm{dz}}{\mathrm{dx}}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\mathrm{3}\:\frac{\mathrm{dz}}{\mathrm{dx}}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)=−\mathrm{3z} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{dx}}=\:\frac{−\mathrm{z}}{\mathrm{z}^{\mathrm{2}} +\mathrm{x}}= \\ $$$$\:\:\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{z}}{\mathrm{dx}^{\mathrm{2}} }=\:\frac{−\frac{\mathrm{dz}}{\mathrm{dx}}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)+\mathrm{z}\left(\mathrm{2z}.\frac{\mathrm{dz}}{\mathrm{dx}}+\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:=\:\frac{−\frac{\mathrm{dz}}{\mathrm{dx}}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)+\mathrm{2z}^{\mathrm{2}} \frac{\mathrm{dz}}{\mathrm{dx}}+\mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\:\frac{\frac{\mathrm{dz}}{\mathrm{dx}}\left(\mathrm{2z}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} −\mathrm{x}\right)+\mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} }=\:\frac{\frac{−\mathrm{z}}{\mathrm{z}^{\mathrm{2}} +\mathrm{x}}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{x}\right)+\mathrm{z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} } \\ $$$$\:=\:\frac{\mathrm{xz}−\mathrm{z}^{\mathrm{3}} +\mathrm{z}^{\mathrm{3}} +\mathrm{zx}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} }=\:\frac{\mathrm{2zx}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$\:\mathrm{Again}, \\ $$$$\:\:\:\mathrm{D}.\mathrm{w}.\mathrm{r}.\mathrm{to}.\mathrm{y} \\ $$$$\:\:\mathrm{z}^{\mathrm{3}} +\mathrm{3xz}+\mathrm{3y}=\mathrm{0} \\ $$$$\:\:\mathrm{3z}^{\mathrm{2}} \frac{\mathrm{dz}}{\mathrm{dy}}+\mathrm{3x}\frac{\mathrm{dz}}{\mathrm{dy}}+\mathrm{3}=\mathrm{0} \\ $$$$\:\:\:\:\:\mathrm{3}\frac{\mathrm{dz}}{\mathrm{dy}}\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)=−\mathrm{3} \\ $$$$\:\:\:\:\:\frac{\mathrm{dz}}{\mathrm{dy}}=\:−\mathrm{1}.\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{−\mathrm{1}} \\ $$$$\:\:\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{z}}{\mathrm{dy}^{\mathrm{2}} }=\:−\mathrm{1}.\left(−\mathrm{1}\right)\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{−\mathrm{2}} .\mathrm{2z}\frac{\mathrm{dz}}{\mathrm{dy}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{2z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{2}} }.\frac{−\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{−\mathrm{2z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$\:\mathrm{now}, \\ $$$$\:\:\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial\mathrm{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \mathrm{z}}{\partial^{\mathrm{2}} \mathrm{y}}=\:\frac{\mathrm{2xz}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} }+\frac{−\mathrm{2z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$\:\:=\:\:\frac{\mathrm{2xz}−\mathrm{2z}}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} }=\:\frac{\mathrm{2z}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} } \\ $$$$\: \\ $$$$\:\mathrm{hence} \\ $$$$\:\therefore\:\:\:\frac{\partial^{\mathrm{2}} {z}}{\partial\mathrm{x}^{\mathrm{2}} }+\:\frac{\partial^{\mathrm{2}} {z}}{\partial\mathrm{y}^{\mathrm{2}} }=\:\frac{\mathrm{2z}\left(\mathrm{x}−\mathrm{1}\right)}{\left(\mathrm{z}^{\mathrm{2}} +\mathrm{x}\right)^{\mathrm{3}} }\:\mathrm{Proved}//. \\ $$$$\: \\ $$$$\:\: \\ $$$$\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *