Question Number 48849 by vajpaithegrate@gmail.com last updated on 29/Nov/18
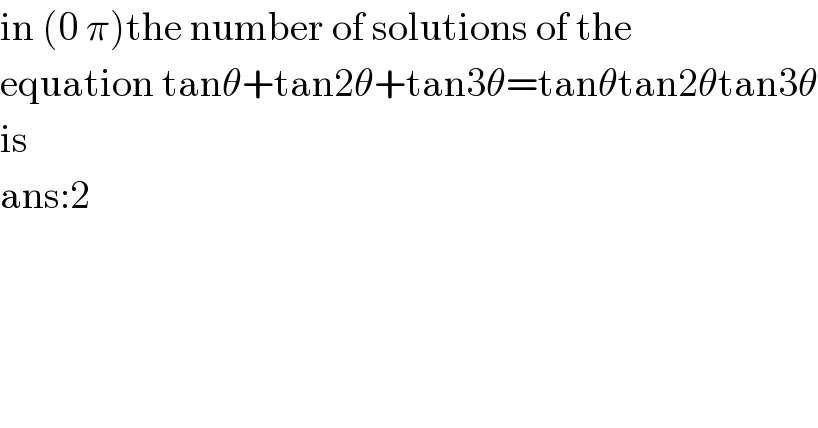
$$\mathrm{in}\:\left(\mathrm{0}\:\pi\right)\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{equation}\:\mathrm{tan}\theta+\mathrm{tan2}\theta+\mathrm{tan3}\theta=\mathrm{tan}\theta\mathrm{tan2}\theta\mathrm{tan3}\theta \\ $$$$\mathrm{is} \\ $$$$\mathrm{ans}:\mathrm{2} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 29/Nov/18

$${tan}\mathrm{3}\theta=\frac{{tan}\mathrm{2}\theta+{tan}\theta}{\mathrm{1}−{tan}\mathrm{2}\theta{tan}\theta} \\ $$$${tan}\mathrm{3}\theta−{tan}\theta{tan}\mathrm{2}\theta{tan}\mathrm{3}\theta={tan}\mathrm{2}\theta+{tan}\theta \\ $$$${tan}\mathrm{3}\theta−{tan}\mathrm{2}\theta−{tan}\theta={tan}\theta{tan}\mathrm{2}\theta{tan}\mathrm{3}\theta \\ $$$${so} \\ $$$${tan}\theta+{tan}\mathrm{2}\theta+{tan}\mathrm{3}\theta={tan}\mathrm{3}\theta−{tan}\mathrm{2}\theta−{tan}\theta \\ $$$$\mathrm{2}\left({tan}\theta+{tan}\mathrm{2}\theta\right)=\mathrm{0} \\ $$$${t}+\frac{\mathrm{2}{t}}{\mathrm{1}−{t}^{\mathrm{2}} }=\mathrm{0}\:\:\:\:{t}={tan}\theta \\ $$$${t}−{t}^{\mathrm{3}} +\mathrm{2}{t}=\mathrm{0} \\ $$$$\mathrm{3}{t}−{t}^{\mathrm{3}} =\mathrm{0} \\ $$$${t}\left(\mathrm{3}−{t}^{\mathrm{2}} \right)= \\ $$$${t}=\mathrm{0} \\ $$$${t}^{\mathrm{2}} =\mathrm{3}\:\:\:{t}=\pm\sqrt{\mathrm{3}}\: \\ $$$$ \\ $$$${given}\:{interval}\:{is}\:\left(\mathrm{0},\pi\right) \\ $$$${so}\:{solution}\:{are} \\ $$$${t}=\pm\sqrt{\mathrm{3}}\: \\ $$$${that}\:{is}\:{tan}\theta=\pm\sqrt{\mathrm{3}}\: \\ $$$${so}\:\theta=\mathrm{60}^{{o}} \:{and}\:\mathrm{120}^{{o}} \\ $$$$\theta=\frac{\pi}{\mathrm{3}},\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$
Commented by vajpaithegrate@gmail.com last updated on 29/Nov/18

$$\mathrm{tnq}\:\mathrm{sir} \\ $$
