In-a-ABC-if-s-a-a-b-s-c-b-c-then-prove-that-r-1-r-2-r-3-are-in-A-P-Here-r-1-r-2-and-r-3-are-the-exradii-opposite-to-angles-A-B-and-C-respectively-

Question Number 16359 by Tinkutara last updated on 21/Jun/17

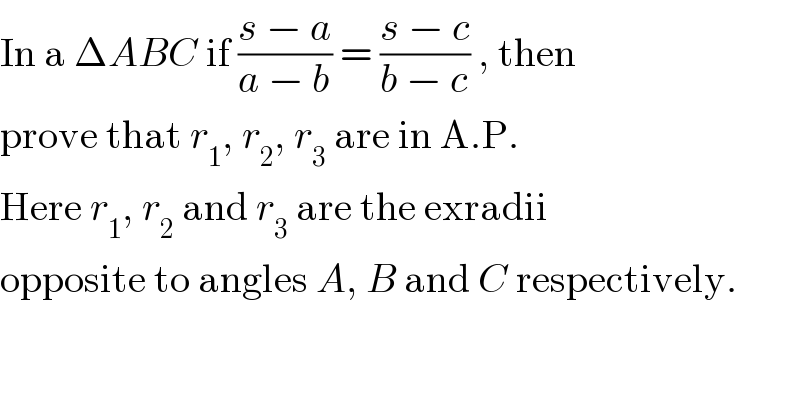
$$\mathrm{In}\:\mathrm{a}\:\Delta{ABC}\:\mathrm{if}\:\frac{{s}\:−\:{a}}{{a}\:−\:{b}}\:=\:\frac{{s}\:−\:{c}}{{b}\:−\:{c}}\:,\:\mathrm{then} \\ $$$$\mathrm{prove}\:\mathrm{that}\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} ,\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{in}\:\mathrm{A}.\mathrm{P}. \\ $$$$\mathrm{Here}\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} \:\mathrm{and}\:{r}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{the}\:\mathrm{exradii} \\ $$$$\mathrm{opposite}\:\mathrm{to}\:\mathrm{angles}\:{A},\:{B}\:\mathrm{and}\:{C}\:\mathrm{respectively}. \\ $$

Answered by ajfour last updated on 21/Jun/17

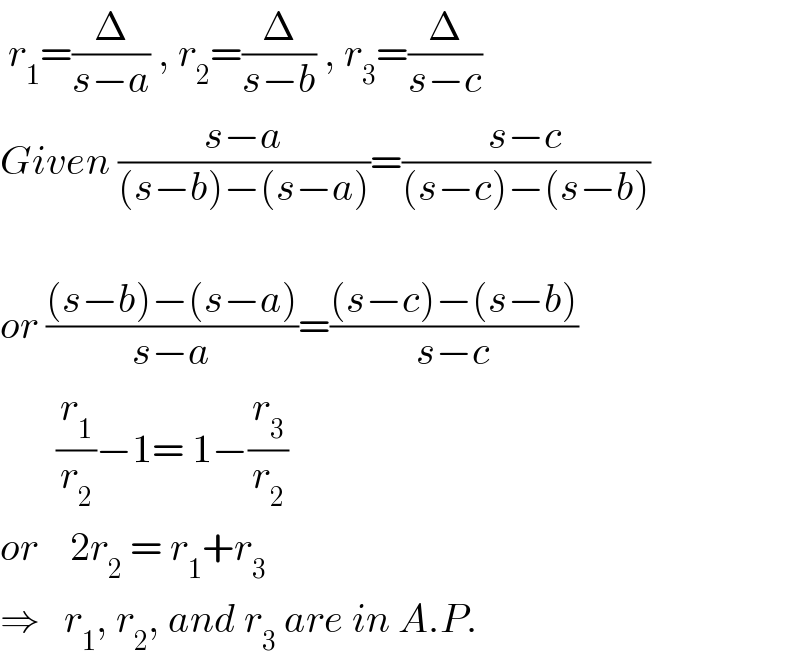
$$\:{r}_{\mathrm{1}} =\frac{\Delta}{{s}−{a}}\:,\:{r}_{\mathrm{2}} =\frac{\Delta}{{s}−{b}}\:,\:{r}_{\mathrm{3}} =\frac{\Delta}{{s}−{c}} \\ $$$${Given}\:\frac{{s}−{a}}{\left({s}−{b}\right)−\left({s}−{a}\right)}=\frac{{s}−{c}}{\left({s}−{c}\right)−\left({s}−{b}\right)} \\ $$$$ \\ $$$${or}\:\frac{\left({s}−{b}\right)−\left({s}−{a}\right)}{{s}−{a}}=\frac{\left({s}−{c}\right)−\left({s}−{b}\right)}{{s}−{c}} \\ $$$$\:\:\:\:\:\:\:\frac{{r}_{\mathrm{1}} }{{r}_{\mathrm{2}} }−\mathrm{1}=\:\mathrm{1}−\frac{{r}_{\mathrm{3}} }{{r}_{\mathrm{2}} } \\ $$$${or}\:\:\:\:\mathrm{2}{r}_{\mathrm{2}} \:=\:{r}_{\mathrm{1}} +{r}_{\mathrm{3}} \: \\ $$$$\Rightarrow\:\:\:{r}_{\mathrm{1}} ,\:{r}_{\mathrm{2}} ,\:{and}\:{r}_{\mathrm{3}} \:{are}\:{in}\:{A}.{P}.\: \\ $$

Commented by Tinkutara last updated on 21/Jun/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com