Question Number 13201 by Tinkutara last updated on 16/May/17
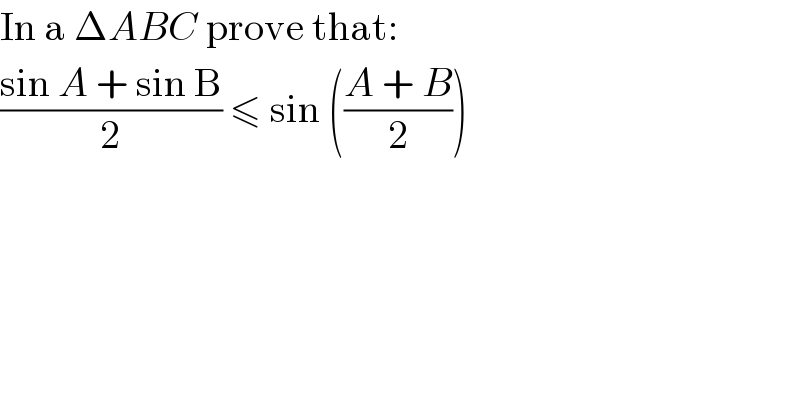
$$\mathrm{In}\:\mathrm{a}\:\Delta{ABC}\:\mathrm{prove}\:\mathrm{that}: \\ $$$$\frac{\mathrm{sin}\:{A}\:+\:\mathrm{sin}\:\mathrm{B}}{\mathrm{2}}\:\leqslant\:\mathrm{sin}\:\left(\frac{{A}\:+\:{B}}{\mathrm{2}}\right) \\ $$
Commented by ajfour last updated on 16/May/17
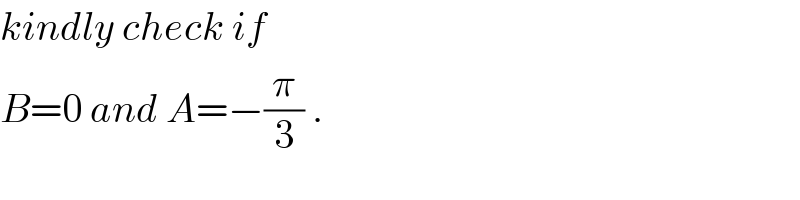
$${kindly}\:{check}\:{if} \\ $$$${B}=\mathrm{0}\:{and}\:{A}=−\frac{\pi}{\mathrm{3}}\:. \\ $$
Answered by ajfour last updated on 16/May/17

$${A}+{B}=\pi−{C} \\ $$$$\frac{{A}+{B}}{\mathrm{2}}\:=\:\frac{\pi}{\mathrm{2}}−\frac{{C}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)=\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\:>\:\mathrm{0}\: \\ $$$$\:\mathrm{sin}\:{A}+\mathrm{sin}\:{B}=\mathrm{2sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right) \\ $$$$\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}}{\mathrm{2sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)}\:=\:\mathrm{cos}\:\left(\frac{{A}−{B}}{\mathrm{2}}\right)\leqslant\mathrm{1} \\ $$$${hence} \\ $$$$\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}}{\mathrm{2}}\:\leqslant\:\mathrm{sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right) \\ $$$$\mathrm{sin}\:\left(\frac{{A}+{B}}{\mathrm{2}}\right)>\mathrm{0}\:\:\:{so}\:{inequality}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{doesn}'{t}\:{change}\:. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
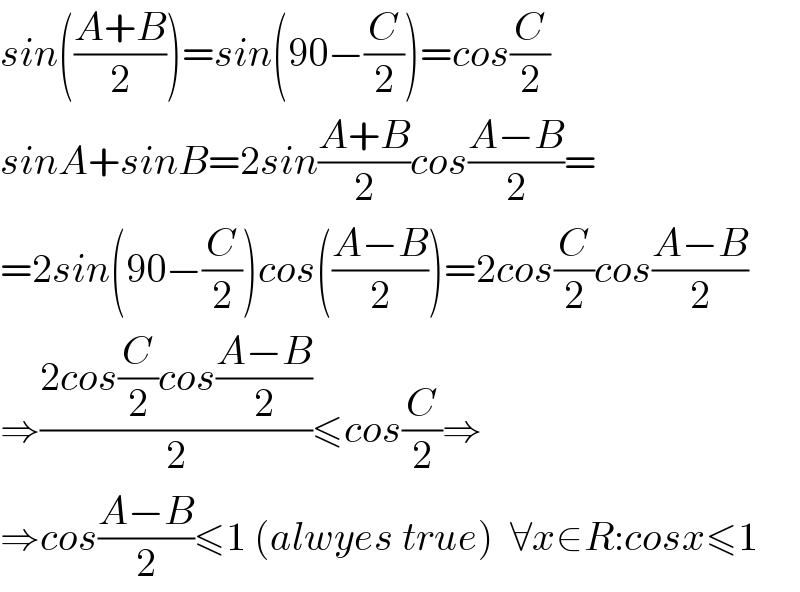
$${sin}\left(\frac{{A}+{B}}{\mathrm{2}}\right)={sin}\left(\mathrm{90}−\frac{{C}}{\mathrm{2}}\right)={cos}\frac{{C}}{\mathrm{2}} \\ $$$${sinA}+{sinB}=\mathrm{2}{sin}\frac{{A}+{B}}{\mathrm{2}}{cos}\frac{{A}−{B}}{\mathrm{2}}= \\ $$$$=\mathrm{2}{sin}\left(\mathrm{90}−\frac{{C}}{\mathrm{2}}\right){cos}\left(\frac{{A}−{B}}{\mathrm{2}}\right)=\mathrm{2}{cos}\frac{{C}}{\mathrm{2}}{cos}\frac{{A}−{B}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{cos}\frac{{C}}{\mathrm{2}}{cos}\frac{{A}−{B}}{\mathrm{2}}}{\mathrm{2}}\leqslant{cos}\frac{{C}}{\mathrm{2}}\Rightarrow \\ $$$$\Rightarrow{cos}\frac{{A}−{B}}{\mathrm{2}}\leqslant\mathrm{1}\:\left({alwyes}\:{true}\right)\:\:\forall{x}\in{R}:{cosx}\leqslant\mathrm{1}\: \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17

$${sinA}+{sinB}=\frac{{a}}{\mathrm{2}{R}}+\frac{{b}}{\mathrm{2}{R}}=\frac{{a}+{b}}{\mathrm{2}{R}} \\ $$$${sin}\left(\frac{{A}+{B}}{\mathrm{2}}\right)={cos}\frac{{C}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}+{cosC}}{\mathrm{2}}}= \\ $$$$=\sqrt{\frac{\mathrm{1}+\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}}}{\mathrm{2}}}=\sqrt{\frac{\left({a}+{b}+{c}\right)\left({a}+{b}−{c}\right)}{\mathrm{4}{ab}}} \\ $$$$=\sqrt{\frac{{p}\left({p}−{c}\right)}{{ab}}}\:\:\:\:\:\left({p}=\frac{{a}+{b}+{c}}{\mathrm{2}},{S}=\frac{{abc}}{\mathrm{4}{R}}\right) \\ $$$$\Rightarrow\frac{{a}+{b}}{\mathrm{4}{R}}\leqslant\sqrt{\frac{{p}\left({p}−{c}\right)}{{ab}}}\Rightarrow\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{16}{R}^{\mathrm{2}} }\leqslant\frac{{p}\left({p}−{c}\right)}{{ab}}\Rightarrow \\ $$$$\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\frac{{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} }{{S}^{\mathrm{2}} }}\leqslant\frac{{p}\left({p}−{c}\right)}{{ab}}\Rightarrow{S}^{\mathrm{2}} .\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{abc}^{\mathrm{2}} }\leqslant{p}\left({p}−{c}\right)\Rightarrow \\ $$$${p}\left({p}−{a}\right)\left({p}−{b}\right)\left({p}−{c}\right)\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{abc}^{\mathrm{2}} }\leqslant{p}\left({p}−{c}\right)\Rightarrow \\ $$$$\left({p}−{a}\right)\left({p}−{b}\right)\left({a}+{b}\right)^{\mathrm{2}} \leqslant{abc}^{\mathrm{2}} \Rightarrow \\ $$$$\left({c}+{b}−{a}\right)\left({c}−{b}+{a}\right)\left({a}+{b}\right)^{\mathrm{2}} \leqslant\mathrm{4}{abc}^{\mathrm{2}} \Rightarrow \\ $$$$\left({c}^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} \right)\left({a}+{b}\right)^{\mathrm{2}} \leqslant\mathrm{4}{abc}^{\mathrm{2}} \Rightarrow \\ $$$${c}^{\mathrm{2}} \left(\left({a}+{b}\right)^{\mathrm{2}} −\mathrm{4}{ab}\right)\leqslant\left({b}−{a}\right)^{\mathrm{2}} \left({b}+{a}\right)^{\mathrm{2}} \Rightarrow \\ $$$${c}^{\mathrm{2}} \left({b}−{a}\right)^{\mathrm{2}} \leqslant\left({b}−{a}\right)^{\mathrm{2}} \left({b}+{a}\right)^{\mathrm{2}} \Rightarrow{c}^{\mathrm{2}} \leqslant\left({b}+{a}\right)^{\mathrm{2}} \Rightarrow \\ $$$${c}\leqslant{b}+{a}\:\:\:.\blacksquare\:\:\left({proved}\right) \\ $$$${note}:{if}\:\boldsymbol{{a}}=\boldsymbol{{b}}\Rightarrow\frac{{sinA}+{sinB}}{\mathrm{2}}={sinA}\leqslant{sin}\left(\frac{{A}+{A}}{\mathrm{2}}\right)={sinA}. \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
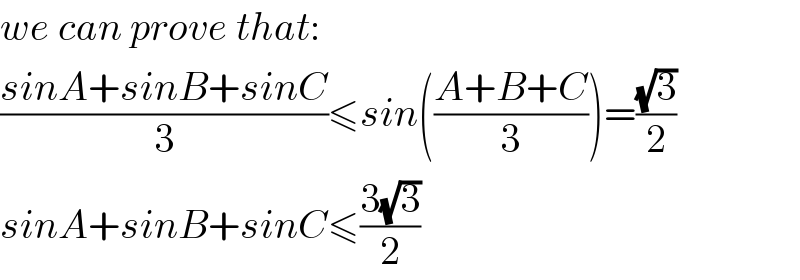
$${we}\:{can}\:{prove}\:{that}: \\ $$$$\frac{{sinA}+{sinB}+{sinC}}{\mathrm{3}}\leqslant{sin}\left(\frac{{A}+{B}+{C}}{\mathrm{3}}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${sinA}+{sinB}+{sinC}\leqslant\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 16/May/17
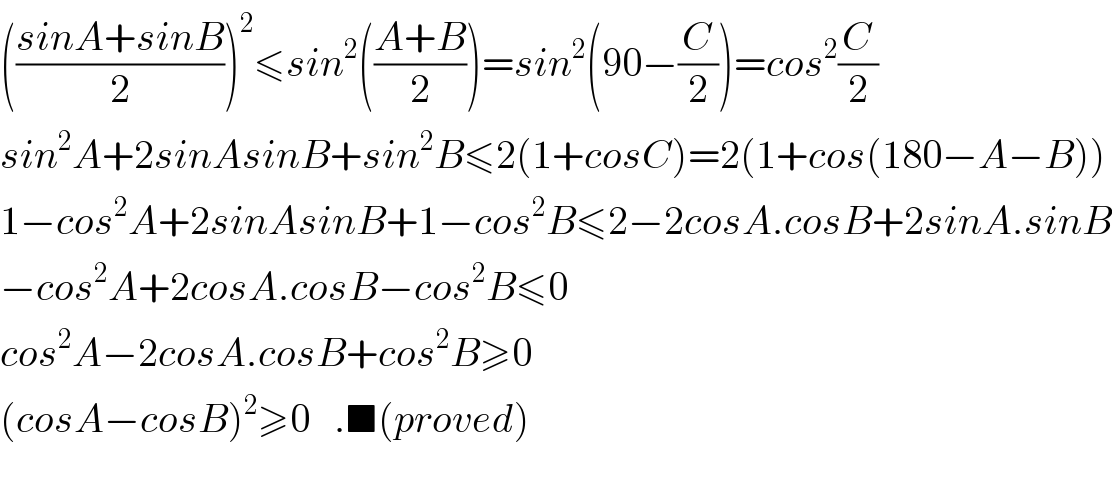
$$\left(\frac{{sinA}+{sinB}}{\mathrm{2}}\right)^{\mathrm{2}} \leqslant{sin}^{\mathrm{2}} \left(\frac{{A}+{B}}{\mathrm{2}}\right)={sin}^{\mathrm{2}} \left(\mathrm{90}−\frac{{C}}{\mathrm{2}}\right)={cos}^{\mathrm{2}} \frac{{C}}{\mathrm{2}} \\ $$$${sin}^{\mathrm{2}} {A}+\mathrm{2}{sinAsinB}+{sin}^{\mathrm{2}} {B}\leqslant\mathrm{2}\left(\mathrm{1}+{cosC}\right)=\mathrm{2}\left(\mathrm{1}+{cos}\left(\mathrm{180}−{A}−{B}\right)\right) \\ $$$$\mathrm{1}−{cos}^{\mathrm{2}} {A}+\mathrm{2}{sinAsinB}+\mathrm{1}−{cos}^{\mathrm{2}} {B}\leqslant\mathrm{2}−\mathrm{2}{cosA}.{cosB}+\mathrm{2}{sinA}.{sinB} \\ $$$$−{cos}^{\mathrm{2}} {A}+\mathrm{2}{cosA}.{cosB}−{cos}^{\mathrm{2}} {B}\leqslant\mathrm{0} \\ $$$${cos}^{\mathrm{2}} {A}−\mathrm{2}{cosA}.{cosB}+{cos}^{\mathrm{2}} {B}\geqslant\mathrm{0} \\ $$$$\left({cosA}−{cosB}\right)^{\mathrm{2}} \geqslant\mathrm{0}\:\:\:.\blacksquare\left({proved}\right) \\ $$$$ \\ $$
