Question Number 104110 by joki last updated on 19/Jul/20

$${in}\:{a}\:{box}\:{A}\:{there}\:{are}\:\mathrm{3}\:{red}\:{balls}\:{and}\:\mathrm{2}\:{white} \\ $$$${balls}.{while}\:{in}\:{box}\:{B}\:{there}\:{are}\:\mathrm{4}\:{red}\:{balls}\:{and} \\ $$$$\mathrm{5}\:{white}\:{balls}.{if}\:{from}\:{boxA}\:{and}\:{B}\:{each}\:{are}\: \\ $$$${taken}\:{two}\:{balls}\:{one}\:{by}\:{one}\:{with}\:{return}\:.\:{the}\: \\ $$$${chance}\:{of}\:{being}\:{taken}\:{is}\:{one}\:{white}\:{ball}? \\ $$$${a}.\frac{\mathrm{4}}{\mathrm{675}}\:\:\:\:\:{c}.\frac{\mathrm{128}}{\mathrm{675}}\:\:\:\:\:\:{e}.\frac{\mathrm{218}}{\mathrm{675}} \\ $$$${b}.\frac{\mathrm{64}}{\mathrm{675}}\:\:\:\:\:\:{d}.\frac{\mathrm{184}}{\mathrm{675}} \\ $$$$ \\ $$$$ \\ $$
Answered by bobhans last updated on 19/Jul/20
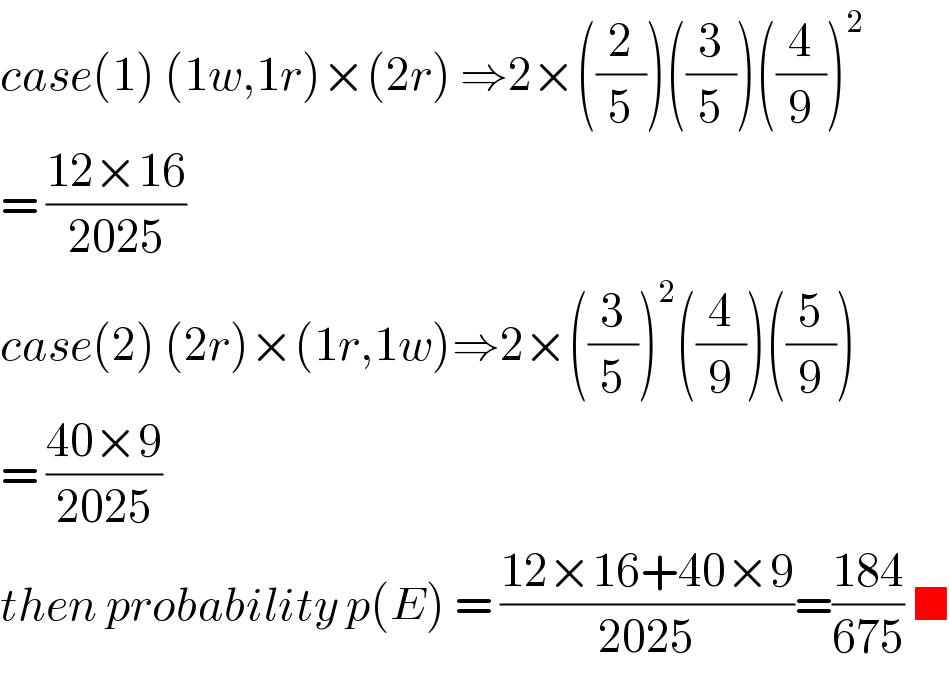
$${case}\left(\mathrm{1}\right)\:\left(\mathrm{1}{w},\mathrm{1}{r}\right)×\left(\mathrm{2}{r}\right)\:\Rightarrow\mathrm{2}×\left(\frac{\mathrm{2}}{\mathrm{5}}\right)\left(\frac{\mathrm{3}}{\mathrm{5}}\right)\left(\frac{\mathrm{4}}{\mathrm{9}}\right)^{\mathrm{2}} \\ $$$$=\:\frac{\mathrm{12}×\mathrm{16}}{\mathrm{2025}} \\ $$$${case}\left(\mathrm{2}\right)\:\left(\mathrm{2}{r}\right)×\left(\mathrm{1}{r},\mathrm{1}{w}\right)\Rightarrow\mathrm{2}×\left(\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} \left(\frac{\mathrm{4}}{\mathrm{9}}\right)\left(\frac{\mathrm{5}}{\mathrm{9}}\right) \\ $$$$=\:\frac{\mathrm{40}×\mathrm{9}}{\mathrm{2025}} \\ $$$${then}\:{probability}\:{p}\left({E}\right)\:=\:\frac{\mathrm{12}×\mathrm{16}+\mathrm{40}×\mathrm{9}}{\mathrm{2025}}=\frac{\mathrm{184}}{\mathrm{675}}\:\blacksquare \\ $$
