In-a-by-election-20-of-the-electorate-voted-for-Mr-X-If-5-voters-are-chosen-at-random-from-this-electorate-what-is-the-probability-that-20-of-the-sample-voted-for-Mr-X-a-1-b-1-5-c-

Question Number 105812 by Ar Brandon last updated on 31/Jul/20

$$\mathrm{In}\:\mathrm{a}\:\mathrm{by}-\mathrm{election}\:\mathrm{20\%}\:\mathrm{of}\:\mathrm{the}\:\mathrm{electorate}\:\mathrm{voted}\:\mathrm{for}\:\mathrm{Mr}\:\mathrm{X}. \\ $$$$\mathrm{If}\:\mathrm{5}\:\mathrm{voters}\:\mathrm{are}\:\mathrm{chosen}\:\mathrm{at}\:\mathrm{random}\:\mathrm{from}\:\mathrm{this}\:\mathrm{electorate},\:\mathrm{what} \\ $$$$\mathrm{is}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{20\%}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sample}\:\mathrm{voted}\:\mathrm{for}\:\mathrm{Mr}\:\mathrm{X}\:? \\ $$$$\left(\mathrm{a}\right)\:\mathrm{1}\:\:\:\:\left(\mathrm{b}\right)\:\frac{\mathrm{1}}{\mathrm{5}}\:\:\:\:\left(\mathrm{c}\right)\:\frac{\mathrm{1}}{\mathrm{625}}\:\:\:\:\left(\mathrm{d}\right)\:\frac{\mathrm{256}}{\mathrm{625}} \\ $$

Answered by Don08q last updated on 31/Jul/20

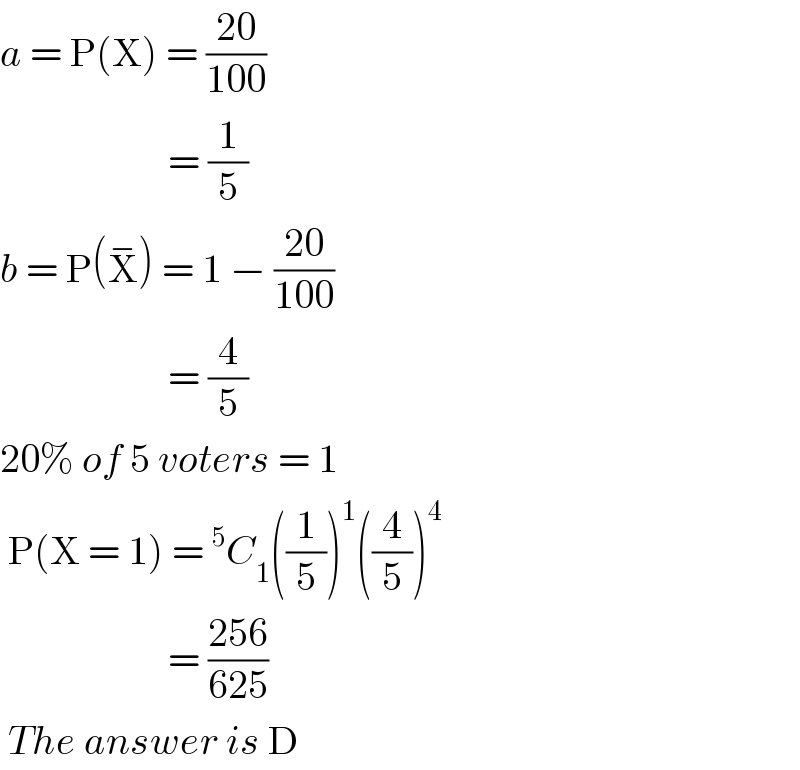
$${a}\:=\:\mathrm{P}\left(\mathrm{X}\right)\:=\:\frac{\mathrm{20}}{\mathrm{100}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{5}} \\ $$$${b}\:=\:\mathrm{P}\left(\overset{−} {\mathrm{X}}\right)\:=\:\mathrm{1}\:−\:\frac{\mathrm{20}}{\mathrm{100}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{4}}{\mathrm{5}} \\ $$$$\mathrm{20\%}\:{of}\:\mathrm{5}\:{voters}\:=\:\mathrm{1} \\ $$$$\:\mathrm{P}\left(\mathrm{X}\:=\:\mathrm{1}\right)\:=\:^{\mathrm{5}} {C}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{5}}\right)^{\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{256}}{\mathrm{625}} \\ $$$$\:{The}\:{answer}\:{is}\:\mathrm{D} \\ $$

Commented by Ar Brandon last updated on 31/Jul/20

$$\mathrm{Thanks} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com