Question Number 99230 by Ar Brandon last updated on 19/Jun/20

$$\ast\backslash\mathcal{I}\mathrm{n}\:\mathrm{a}\:\mathrm{certain}\:\mathrm{country},\:\mathrm{4}\:\mathrm{people}\:\mathrm{are}\:\mathrm{tested}\:\mathrm{positive}\:\mathrm{for}\:\mathrm{the}\:\mathrm{covid}−\mathrm{19}\:\mathrm{per}\:\mathrm{hour}. \\ $$$$\mathcal{D}\mathrm{etermine}\:\mathrm{the}\:\mathrm{probability}\:\mathrm{that}\:\mathrm{in}\:\mathrm{an}\:\mathrm{hour}; \\ $$$$\mathrm{a}\backslash\mathrm{Exactly}\:\mathrm{2}\:\mathrm{people}\:\mathrm{are}\:\mathrm{contaminated} \\ $$$$\mathrm{b}\backslash\mathrm{At}\:\mathrm{most}\:\mathrm{one}\:\mathrm{person}\:\mathrm{is}\:\mathrm{contaminated}. \\ $$$$\mathrm{c}\backslash\mathrm{Between}\:\mathrm{2}\:\mathrm{and}\:\mathrm{5}\:\mathrm{people}\:\mathrm{are}\:\mathrm{contaminated}. \\ $$
Commented by john santu last updated on 20/Jun/20
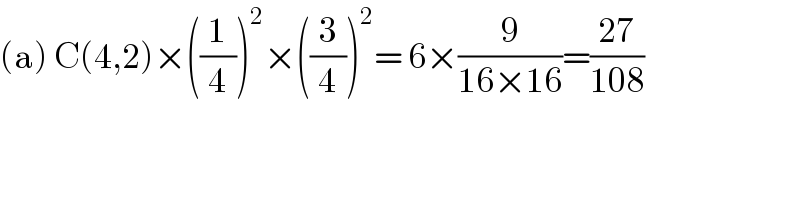
$$\left(\mathrm{a}\right)\:\mathrm{C}\left(\mathrm{4},\mathrm{2}\right)×\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} ×\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\mathrm{6}×\frac{\mathrm{9}}{\mathrm{16}×\mathrm{16}}=\frac{\mathrm{27}}{\mathrm{108}} \\ $$
