Question Number 111277 by Aina Samuel Temidayo last updated on 03/Sep/20

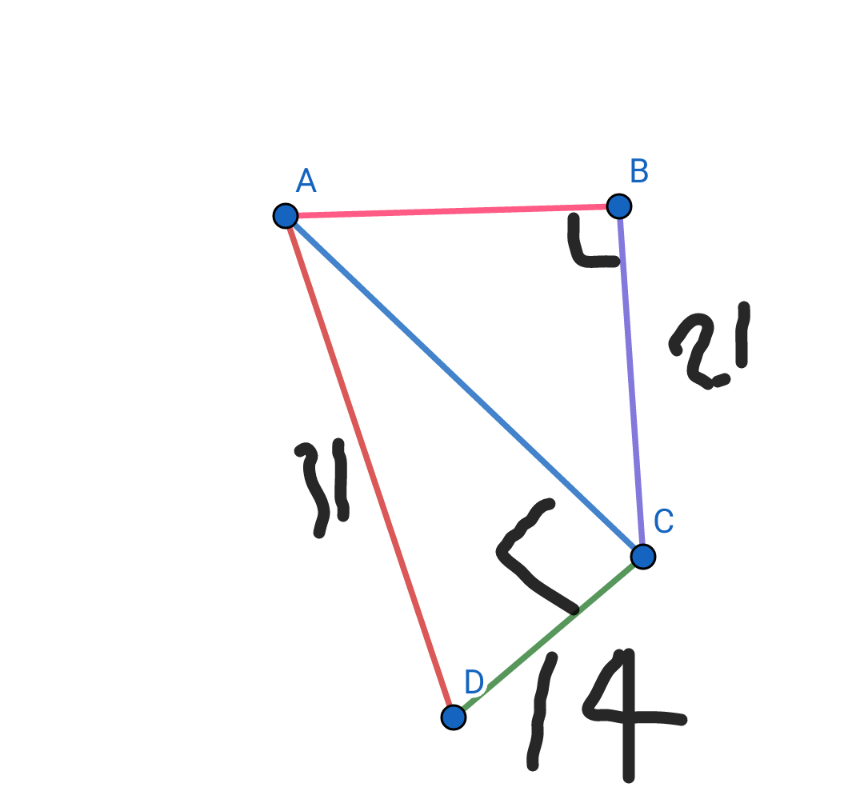
$$\mathrm{In}\:\mathrm{a}\:\mathrm{quadrilateral}\:\mathrm{ABCD},\:\angle\mathrm{B}\:\mathrm{is}\:\mathrm{a} \\ $$$$\mathrm{right}\:\mathrm{angle},\:\mathrm{diagonal}\:\mathrm{AC}\:\mathrm{is} \\ $$$$\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\mathrm{CD},\mathrm{BC}=\mathrm{21cm},\mathrm{CD}=\mathrm{14cm}\:\mathrm{and} \\ $$$$\mathrm{AD}=\mathrm{31cm}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{ABCD}. \\ $$
Answered by 1549442205PVT last updated on 03/Sep/20
Commented by 1549442205PVT last updated on 03/Sep/20

$$\mathrm{Apply}\:\mathrm{Pythagor}'\mathrm{s}\:\mathrm{theorem}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{triangles}\:\mathrm{ACD}\:\mathrm{and}\:\mathrm{ABC}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{AC}=\sqrt{\mathrm{AD}^{\mathrm{2}} −\mathrm{CD}^{\mathrm{2}} }=\sqrt{\mathrm{31}^{\mathrm{2}} −\mathrm{14}^{\mathrm{2}} }=\mathrm{3}\sqrt{\mathrm{85}}\:\left(\mathrm{cm}\right) \\ $$$$\mathrm{AB}=\sqrt{\mathrm{AC}^{\mathrm{2}} −\mathrm{BC}^{\mathrm{2}} }=\sqrt{\mathrm{765}−\mathrm{441}}=\mathrm{18}\left(\mathrm{cm}\right) \\ $$$$\mathrm{The}\:\mathrm{are}\:\mathrm{of}\:\mathrm{the}\:\mathrm{quadrilateral}\:\mathrm{is} \\ $$$$\mathrm{S}=\mathrm{S}_{\mathrm{ABC}} +\mathrm{S}_{\mathrm{ACD}} =\frac{\mathrm{21}.\mathrm{18}}{\mathrm{2}}+\frac{\mathrm{14}.\mathrm{3}\sqrt{\mathrm{85}}}{\mathrm{2}} \\ $$$$=\mathrm{189}+\mathrm{21}\sqrt{\mathrm{85}}\:\left(\mathrm{cm}^{\mathrm{2}} \right) \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20

$$\mathrm{Thanks}. \\ $$
