Menu Close

In-a-tennis-tournament-n-women-and-2n-men-played-Each-player-played-exactly-one-match-with-every-other-player-If-there-are-no-ties-and-the-number-of-the-matches-won-by-women-to-the-number-of-matches

Tinku Tara 0 Comments
Pin




Question Number 111275 by Aina Samuel Temidayo last updated on 03/Sep/20
In a tennis tournament n women and 2n men played. Each player played exactly one match with every other player. If there are no ties and the number of the matches won by women to the number of matches won by men is 7:5, find n.
$$\mathrm{In}\:\mathrm{a}\:\mathrm{tennis}\:\mathrm{tournament}\:\mathrm{n}\:\mathrm{women}\:\mathrm{and} \\ $$$$\mathrm{2n}\:\mathrm{men}\:\mathrm{played}.\:\mathrm{Each}\:\mathrm{player}\:\mathrm{played} \\ $$$$\mathrm{exactly}\:\mathrm{one}\:\mathrm{match}\:\mathrm{with}\:\mathrm{every}\:\mathrm{other} \\ $$$$\mathrm{player}.\:\mathrm{If}\:\mathrm{there}\:\mathrm{are}\:\mathrm{no}\:\mathrm{ties}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{women} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{men} \\ $$$$\mathrm{is}\:\mathrm{7}:\mathrm{5},\:\mathrm{find}\:\mathrm{n}. \\ $$$$ \\ $$
Answered by 1549442205PVT last updated on 04/Sep/20
Since every player played exactly one match with every other player, i)Case in every match one side is men other side is women.Then total number of matches of the tournamen equal to n×2n=2n^2 .From the hypothesis number of the matches won by women to the number of matches won by men is 7:5 and there are no ties we infer that if denote 7k be number of the matches won by women then 5k be number of the matches won by men Therefore 2n^2 =7k+5k=12k⇔n^2 =6k ⇒n^2 ⋮3 ⇒n=3q⇒(3q)^2 =6k ⇒3q^2 =2k ⇒q⋮2,so q=2p ⇒3(2p)^2 =2k⇒k=6p^2 ⇒n^2 =6.6p^(2 ) ⇒n=6p where p ∈N^∗ Thus,n=6,12,18,... ii)Case in every match two players are arbitrary sex.Total number of player parting in tournament is 3n person .Since every player played exactly one match to 3n−1 other players ,total number of the matches is ((3n(3n−1))/2) Therefore we have ((3n(3n−1))/2)=12k(∗) We prove that capacity don′t ocurrs Indeed,number of matches between one side is female and the other side is male is n×2n=2n^2 .Number of matches between two female players is ((n(n−1))/2).Number of matches between two male players is ((2n(2n−1))/2) Hence, number of matches that involving female players is A=2n^2 +((n(n−1))/2). Number of matches that involving male players is B=2n^2 +((2n(2n−1))/2) It is easy to see that (A/B)<1.Therefore don′t ocurrs case that A:B=7:5
$$\:\:\mathrm{Since}\:\mathrm{every}\:\mathrm{player}\:\mathrm{played}\:\mathrm{exactly} \\ $$$$\:\mathrm{one}\:\mathrm{match}\:\mathrm{with}\:\mathrm{every}\:\mathrm{other}\:\mathrm{player}, \\ $$$$\left.\mathrm{i}\right)\mathrm{Case}\:\mathrm{in}\:\mathrm{every}\:\mathrm{match}\:\mathrm{one}\:\mathrm{side}\:\mathrm{is}\:\mathrm{men} \\ $$$$\mathrm{other}\:\mathrm{side}\:\mathrm{is}\:\mathrm{women}.\mathrm{Then} \\ $$$$\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{of}\:\mathrm{the}\:\mathrm{tournamen} \\ $$$$\mathrm{equal}\:\mathrm{to}\:\mathrm{n}×\mathrm{2n}=\mathrm{2n}^{\mathrm{2}} .\mathrm{From}\:\mathrm{the}\:\mathrm{hypothesis} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{women} \\ $$$$\mathrm{to}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{men} \\ $$$$\mathrm{is}\:\mathrm{7}:\mathrm{5}\:\mathrm{and}\:\mathrm{there}\:\mathrm{are}\:\mathrm{no}\:\mathrm{ties}\:\mathrm{we}\:\mathrm{infer}\:\mathrm{that} \\ $$$$\mathrm{if}\:\mathrm{denote}\:\mathrm{7k}\:\mathrm{be} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{women} \\ $$$$\mathrm{then}\:\mathrm{5k}\:\mathrm{be} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{won}\:\mathrm{by}\:\mathrm{men} \\ $$$$\mathrm{Therefore}\:\mathrm{2n}^{\mathrm{2}} =\mathrm{7k}+\mathrm{5k}=\mathrm{12k}\Leftrightarrow\mathrm{n}^{\mathrm{2}} =\mathrm{6k} \\ $$$$\Rightarrow\mathrm{n}^{\mathrm{2}} \vdots\mathrm{3}\:\Rightarrow\mathrm{n}=\mathrm{3q}\Rightarrow\left(\mathrm{3q}\right)^{\mathrm{2}} =\mathrm{6k} \\ $$$$\Rightarrow\mathrm{3q}^{\mathrm{2}} =\mathrm{2k}\:\Rightarrow\mathrm{q}\vdots\mathrm{2},\mathrm{so}\:\mathrm{q}=\mathrm{2p} \\ $$$$\Rightarrow\mathrm{3}\left(\mathrm{2p}\right)^{\mathrm{2}} =\mathrm{2k}\Rightarrow\mathrm{k}=\mathrm{6p}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{n}^{\mathrm{2}} =\mathrm{6}.\mathrm{6p}^{\mathrm{2}\:} \Rightarrow\mathrm{n}=\mathrm{6p}\:\mathrm{where}\:\mathrm{p}\:\in\mathbb{N}^{\ast} \\ $$$$\boldsymbol{\mathrm{Thus}},\mathrm{n}=\mathrm{6},\mathrm{12},\mathrm{18},… \\ $$$$\left.\mathrm{ii}\right)\mathrm{Case}\:\mathrm{in}\:\mathrm{every}\:\mathrm{match}\:\mathrm{two}\:\mathrm{players}\:\mathrm{are} \\ $$$$\mathrm{arbitrary}\:\mathrm{sex}.\mathrm{Total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{player} \\ $$$$\mathrm{parting}\:\mathrm{in}\:\mathrm{tournament}\:\mathrm{is}\:\mathrm{3n}\:\mathrm{person} \\ $$$$.\mathrm{Since}\:\mathrm{every}\:\mathrm{player}\:\mathrm{played}\:\mathrm{exactly}\:\mathrm{one} \\ $$$$\mathrm{match}\:\mathrm{to}\:\mathrm{3n}−\mathrm{1}\:\mathrm{other}\:\mathrm{players}\:,\mathrm{total} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{the}\:\mathrm{matches}\:\mathrm{is}\:\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{Therefore}\:\mathrm{we}\:\mathrm{have}\:\:\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}}=\mathrm{12k}\left(\ast\right) \\ $$$$\mathrm{We}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{capacity}\:\mathrm{don}'\mathrm{t}\:\mathrm{ocurrs} \\ $$$$\mathrm{Indeed},\mathrm{number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{between} \\ $$$$\mathrm{one}\:\mathrm{side}\:\mathrm{is}\:\mathrm{female}\:\mathrm{and}\:\mathrm{the}\:\mathrm{other}\:\mathrm{side} \\ $$$$\mathrm{is}\:\mathrm{male}\:\mathrm{is}\:\mathrm{n}×\mathrm{2n}=\mathrm{2n}^{\mathrm{2}} .\mathrm{Number}\:\mathrm{of} \\ $$$$\mathrm{matches}\:\mathrm{between}\:\mathrm{two}\:\mathrm{female}\:\:\mathrm{players}\: \\ $$$$\mathrm{is}\:\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}.\mathrm{Number}\:\mathrm{of}\:\mathrm{matches} \\ $$$$\mathrm{between}\:\mathrm{two}\:\mathrm{male}\:\mathrm{players}\:\mathrm{is}\:\frac{\mathrm{2n}\left(\mathrm{2n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{Hence},\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{that}\:\mathrm{involving} \\ $$$$\mathrm{female}\:\mathrm{players}\:\mathrm{is}\:\mathrm{A}=\mathrm{2n}^{\mathrm{2}} +\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)}{\mathrm{2}}. \\ $$$$\:\mathrm{Number}\:\mathrm{of}\:\mathrm{matches}\:\mathrm{that}\:\mathrm{involving} \\ $$$$\mathrm{male}\:\mathrm{players}\:\mathrm{is}\:\mathrm{B}=\mathrm{2n}^{\mathrm{2}} +\frac{\mathrm{2n}\left(\mathrm{2n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\frac{\mathrm{A}}{\mathrm{B}}<\mathrm{1}.\mathrm{Therefore} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{ocurrs}\:\mathrm{case}\:\mathrm{that}\:\mathrm{A}:\mathrm{B}=\mathrm{7}:\mathrm{5} \\ $$
Commented by 1549442205PVT last updated on 04/Sep/20
Here question isn′t clear.If in every match one side is women and other is men then total number of matches equal to n×2n=2n^2 If in one match two player are arbitrary(both are female or both are male or this side is male and other is female)then total number of matches will be ((3n(3n−1))/2)
$$\mathrm{Here}\:\mathrm{question}\:\mathrm{isn}'\mathrm{t}\:\mathrm{clear}.\mathrm{If}\:\mathrm{in}\:\mathrm{every}\:\mathrm{match}\:\mathrm{one}\:\mathrm{side}\:\mathrm{is} \\ $$$$\mathrm{women}\:\mathrm{and}\:\mathrm{other}\:\mathrm{is}\:\mathrm{men}\:\mathrm{then}\:\mathrm{total}\:\:\mathrm{number} \\ $$$$\mathrm{of}\:\mathrm{matches}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{n}×\mathrm{2n}=\mathrm{2n}^{\mathrm{2}} \\ $$$$\mathrm{If}\:\mathrm{in}\:\mathrm{one}\:\mathrm{match}\:\mathrm{two}\:\mathrm{player}\:\mathrm{are} \\ $$$$\mathrm{arbitrary}\left(\mathrm{both}\:\mathrm{are}\:\mathrm{female}\:\mathrm{or}\:\mathrm{both}\:\mathrm{are}\right. \\ $$$$\mathrm{male}\:\mathrm{or}\:\mathrm{this}\:\mathrm{side}\:\mathrm{is}\:\mathrm{male}\:\mathrm{and}\:\mathrm{other}\:\mathrm{is} \\ $$$$\left.\mathrm{female}\right)\mathrm{then}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches} \\ $$$$\mathrm{will}\:\mathrm{be}\:\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
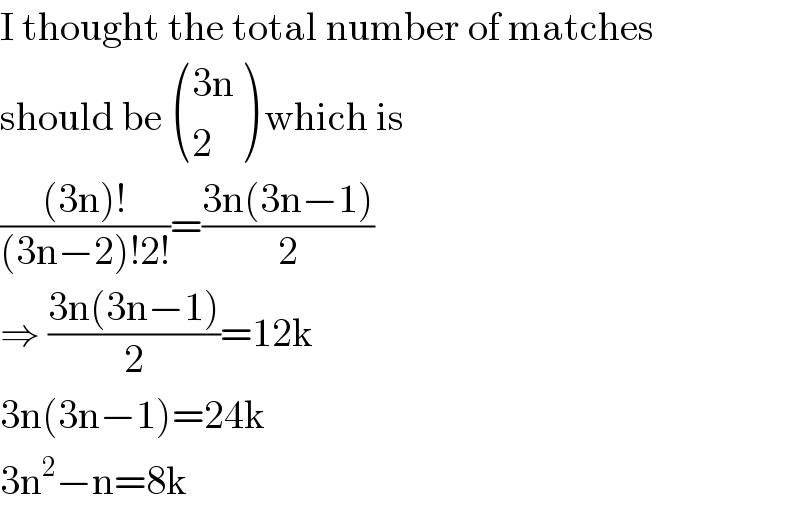
I thought the total number of matches should be (((3n)),(2) ) which is (((3n)!)/((3n−2)!2!))=((3n(3n−1))/2) ⇒ ((3n(3n−1))/2)=12k 3n(3n−1)=24k 3n^2 −n=8k
$$\mathrm{I}\:\mathrm{thought}\:\mathrm{the}\:\mathrm{total}\:\mathrm{number}\:\mathrm{of}\:\mathrm{matches} \\ $$$$\mathrm{should}\:\mathrm{be}\:\begin{pmatrix}{\mathrm{3n}}\\{\mathrm{2}}\end{pmatrix}\:\mathrm{which}\:\mathrm{is} \\ $$$$\frac{\left(\mathrm{3n}\right)!}{\left(\mathrm{3n}−\mathrm{2}\right)!\mathrm{2}!}=\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)}{\mathrm{2}}=\mathrm{12k} \\ $$$$\mathrm{3n}\left(\mathrm{3n}−\mathrm{1}\right)=\mathrm{24k} \\ $$$$\mathrm{3n}^{\mathrm{2}} −\mathrm{n}=\mathrm{8k} \\ $$
Commented by Aina Samuel Temidayo last updated on 03/Sep/20
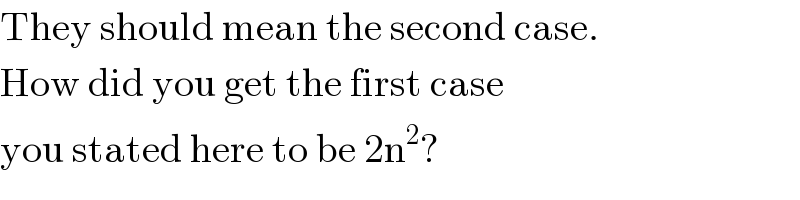
They should mean the second case. How did you get the first case you stated here to be 2n^2 ?
$$\mathrm{They}\:\mathrm{should}\:\mathrm{mean}\:\mathrm{the}\:\mathrm{second}\:\mathrm{case}. \\ $$$$\mathrm{How}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{the}\:\mathrm{first}\:\mathrm{case} \\ $$$$\mathrm{you}\:\mathrm{stated}\:\mathrm{here}\:\mathrm{to}\:\mathrm{be}\:\mathrm{2n}^{\mathrm{2}} ? \\ $$
Commented by 1549442205PVT last updated on 04/Sep/20
Because every female played exactly one match to one male player Thus,here we need understand that the tennis tournament is between male and female.
$$\mathrm{Because}\:\mathrm{every}\:\mathrm{female}\:\mathrm{played}\:\mathrm{exactly} \\ $$$$\mathrm{one}\:\mathrm{match}\:\mathrm{to}\:\mathrm{one}\:\mathrm{male}\:\mathrm{player} \\ $$$$\mathrm{Thus},\mathrm{here}\:\mathrm{we}\:\mathrm{need}\:\mathrm{understand}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{tennis}\:\mathrm{tournament}\:\mathrm{is}\:\mathrm{between} \\ $$$$\mathrm{male}\:\mathrm{and}\:\mathrm{female}. \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20
Ok.
$$\mathrm{Ok}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *