Menu Close

In-a-trapezoid-ABCD-sides-AB-and-CD-are-parallel-and-side-BC-CD-5-If-DC-B-120-and-BA-D-60-Find-the-area-of-ABCD-

Tinku Tara 0 Comments
Pin




Question Number 111539 by Aina Samuel Temidayo last updated on 04/Sep/20
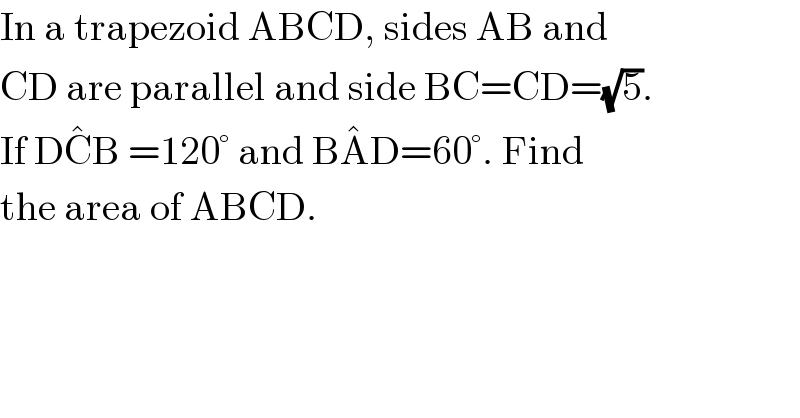
In a trapezoid ABCD, sides AB and CD are parallel and side BC=CD=(√5). If DC^� B =120° and BA^� D=60°. Find the area of ABCD.
$$\mathrm{In}\:\mathrm{a}\:\mathrm{trapezoid}\:\mathrm{ABCD},\:\mathrm{sides}\:\mathrm{AB}\:\mathrm{and} \\ $$$$\mathrm{CD}\:\mathrm{are}\:\mathrm{parallel}\:\mathrm{and}\:\mathrm{side}\:\mathrm{BC}=\mathrm{CD}=\sqrt{\mathrm{5}}. \\ $$$$\mathrm{If}\:\mathrm{D}\hat {\mathrm{C}B}\:=\mathrm{120}°\:\mathrm{and}\:\mathrm{B}\hat {\mathrm{A}D}=\mathrm{60}°.\:\mathrm{Find} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{ABCD}. \\ $$
Answered by 1549442205PVT last updated on 04/Sep/20
Commented by 1549442205PVT last updated on 04/Sep/20
Draw the line d parallel to BC cutting AB at point E.Then BCDE is parallelogram ,so from the hypothesis BC=CD=(√(5 )) and DAB^(�) =60° we have DE=BC=(√5) ,DEA^(�) =CBA^(�) =60°(since BCD^(�) =60°)It follows that ΔADE is equilateralu (since it has two angles equal to 60°).From DF=(((√5).(√3))/2)=((√(15))/2) (DF is the altitude of the equilateral triangle)AB=AE+BE=2(√5) Therefore,S_(ABCD) =((AB+CD)/2)×DF =((2(√5)+(√5))/2)×((√(15))/2)=((3(√(75)))/4)=((15(√3))/4) (cm^2 )
$$\mathrm{Draw}\:\mathrm{the}\:\mathrm{line}\:\mathrm{d}\:\mathrm{parallel}\:\mathrm{to}\:\mathrm{BC}\:\mathrm{cutting} \\ $$$$\mathrm{AB}\:\mathrm{at}\:\mathrm{point}\:\mathrm{E}.\mathrm{Then}\:\mathrm{BCDE}\:\mathrm{is} \\ $$$$\mathrm{parallelogram}\:,\mathrm{so}\:\mathrm{from}\:\mathrm{the}\:\mathrm{hypothesis} \\ $$$$\mathrm{BC}=\mathrm{CD}=\sqrt{\mathrm{5}\:}\:\mathrm{and}\:\widehat {\mathrm{DAB}}=\mathrm{60}°\:\mathrm{we}\:\mathrm{have}\: \\ $$$$\mathrm{DE}=\mathrm{BC}=\sqrt{\mathrm{5}}\:\widehat {,\mathrm{DEA}}=\widehat {\mathrm{CBA}}=\mathrm{60}°\left(\mathrm{since}\right. \\ $$$$\left.\widehat {\mathrm{BCD}}=\mathrm{60}°\right)\mathrm{It}\:\mathrm{follows}\:\mathrm{that}\:\Delta\mathrm{ADE}\:\mathrm{is} \\ $$$$\mathrm{equilateralu}\:\left(\mathrm{since}\:\mathrm{it}\:\mathrm{has}\:\mathrm{two}\:\mathrm{angles}\right. \\ $$$$\left.\mathrm{equal}\:\mathrm{to}\:\mathrm{60}°\right).\mathrm{From}\:\mathrm{DF}=\frac{\sqrt{\mathrm{5}}.\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{15}}}{\mathrm{2}} \\ $$$$\left(\mathrm{DF}\:\mathrm{is}\:\mathrm{the}\:\mathrm{altitude}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equilateral}\right. \\ $$$$\left.\mathrm{triangle}\right)\mathrm{AB}=\mathrm{AE}+\mathrm{BE}=\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\mathrm{Therefore},\mathrm{S}_{\mathrm{ABCD}} =\frac{\mathrm{AB}+\mathrm{CD}}{\mathrm{2}}×\mathrm{DF} \\ $$$$=\frac{\mathrm{2}\sqrt{\mathrm{5}}+\sqrt{\mathrm{5}}}{\mathrm{2}}×\frac{\sqrt{\mathrm{15}}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{75}}}{\mathrm{4}}=\frac{\mathrm{15}\sqrt{\mathrm{3}}}{\mathrm{4}}\:\:\left(\mathrm{cm}^{\mathrm{2}} \right) \\ $$
Commented by Aina Samuel Temidayo last updated on 04/Sep/20
Thanks.
$$\mathrm{Thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *