Question Number 18501 by Tinkutara last updated on 22/Jul/17
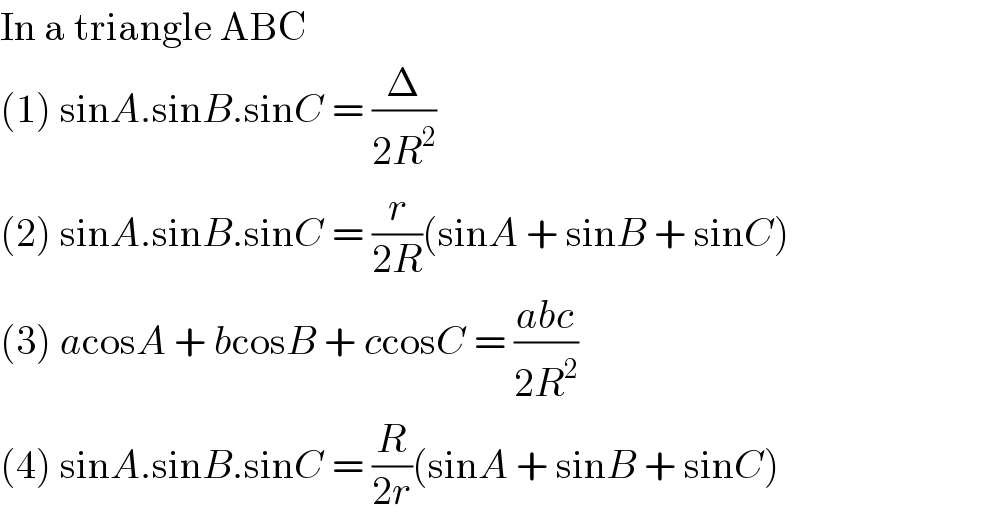
$$\mathrm{In}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{ABC} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{sin}{A}.\mathrm{sin}{B}.\mathrm{sin}{C}\:=\:\frac{\Delta}{\mathrm{2}{R}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}\right)\:\mathrm{sin}{A}.\mathrm{sin}{B}.\mathrm{sin}{C}\:=\:\frac{{r}}{\mathrm{2}{R}}\left(\mathrm{sin}{A}\:+\:\mathrm{sin}{B}\:+\:\mathrm{sin}{C}\right) \\ $$$$\left(\mathrm{3}\right)\:{a}\mathrm{cos}{A}\:+\:{b}\mathrm{cos}{B}\:+\:{c}\mathrm{cos}{C}\:=\:\frac{{abc}}{\mathrm{2}{R}^{\mathrm{2}} } \\ $$$$\left(\mathrm{4}\right)\:\mathrm{sin}{A}.\mathrm{sin}{B}.\mathrm{sin}{C}\:=\:\frac{{R}}{\mathrm{2}{r}}\left(\mathrm{sin}{A}\:+\:\mathrm{sin}{B}\:+\:\mathrm{sin}{C}\right) \\ $$
Commented by b.e.h.i.8.3.417@gmail.com last updated on 22/Jul/17
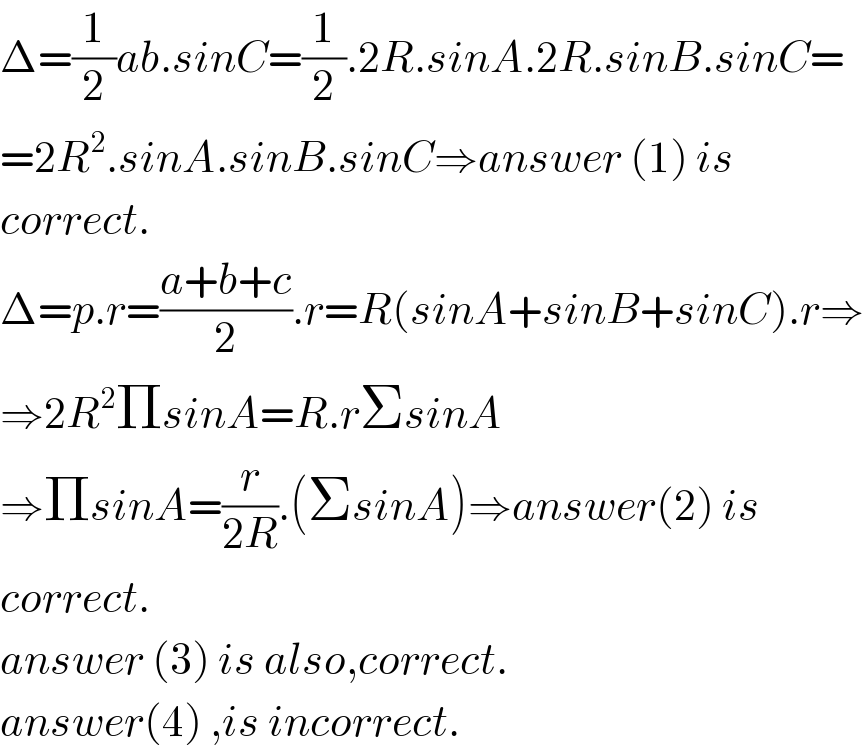
$$\Delta=\frac{\mathrm{1}}{\mathrm{2}}{ab}.{sinC}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}{R}.{sinA}.\mathrm{2}{R}.{sinB}.{sinC}= \\ $$$$=\mathrm{2}{R}^{\mathrm{2}} .{sinA}.{sinB}.{sinC}\Rightarrow{answer}\:\left(\mathrm{1}\right)\:{is} \\ $$$${correct}. \\ $$$$\Delta={p}.{r}=\frac{{a}+{b}+{c}}{\mathrm{2}}.{r}={R}\left({sinA}+{sinB}+{sinC}\right).{r}\Rightarrow \\ $$$$\Rightarrow\mathrm{2}{R}^{\mathrm{2}} \Pi{sinA}={R}.{r}\Sigma{sinA} \\ $$$$\Rightarrow\Pi{sinA}=\frac{{r}}{\mathrm{2}{R}}.\left(\Sigma{sinA}\right)\Rightarrow{answer}\left(\mathrm{2}\right)\:{is} \\ $$$${correct}. \\ $$$${answer}\:\left(\mathrm{3}\right)\:{is}\:{also},{correct}. \\ $$$${answer}\left(\mathrm{4}\right)\:,{is}\:{incorrect}. \\ $$
Commented by Tinkutara last updated on 23/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
