Question Number 170856 by mnjuly1970 last updated on 01/Jun/22
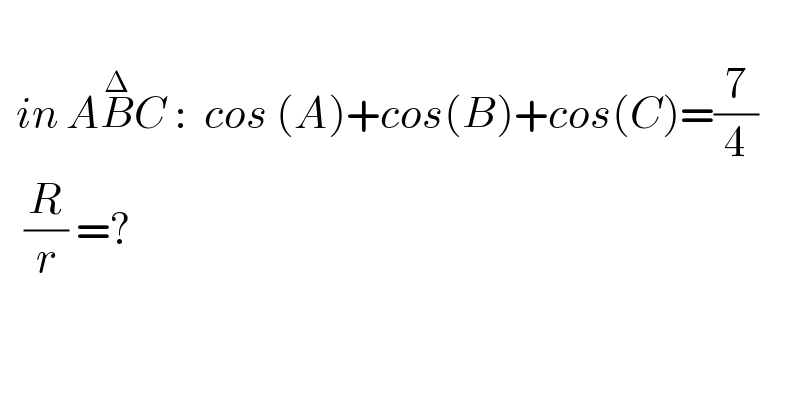
$$ \\ $$$$\:\:{in}\:{A}\overset{\Delta} {{B}C}\::\:\:{cos}\:\left({A}\right)+{cos}\left({B}\right)+{cos}\left({C}\right)=\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\:\:\:\frac{{R}}{{r}}\:=? \\ $$
Commented by mr W last updated on 01/Jun/22

$$\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}=\frac{\mathrm{7}}{\mathrm{4}}\:{not}\:{possible}, \\ $$$${since}\:\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}\leqslant\frac{\mathrm{3}}{\mathrm{2}}. \\ $$
Commented by mnjuly1970 last updated on 02/Jun/22
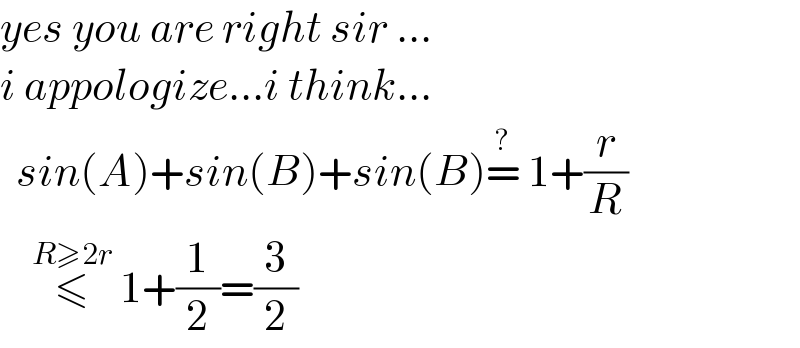
$${yes}\:{you}\:{are}\:{right}\:{sir}\:… \\ $$$${i}\:{appologize}…{i}\:{think}… \\ $$$$\:\:{sin}\left({A}\right)+{sin}\left({B}\right)+{sin}\left({B}\right)\overset{?} {=}\:\mathrm{1}+\frac{{r}}{{R}} \\ $$$$\:\:\:\:\overset{{R}\geqslant\mathrm{2}{r}} {\leqslant}\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\: \\ $$
Answered by mr W last updated on 01/Jun/22

$${assume}\:\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}=\frac{\mathrm{5}}{\mathrm{4}}. \\ $$$$ \\ $$$${a}=\mathrm{2}{R}\:\mathrm{sin}\:{A},\:{b}=\mathrm{2}{R}\:\mathrm{sin}\:{B},\:{c}=\mathrm{2}{R}\:\mathrm{sin}\:{C} \\ $$$$\Delta=\frac{{ab}\:\mathrm{sin}\:{C}}{\mathrm{2}} \\ $$$${r}=\frac{\mathrm{2}\Delta}{{a}+{b}+{c}} \\ $$$$\frac{{R}}{{r}}=\frac{{R}\left({a}+{b}+{c}\right)}{\mathrm{2}\Delta} \\ $$$$\frac{{R}}{{r}}=\frac{{R}\left({a}+{b}+{c}\right)}{{ab}\:\mathrm{sin}\:{C}} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{2}{R}^{\mathrm{2}} \left(\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}\right)}{\mathrm{4}{R}^{\mathrm{2}} \:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{sin}\:{A}+\mathrm{sin}\:{B}+\mathrm{sin}\:{C}}{\mathrm{2}\:\mathrm{sin}\:{A}\:\mathrm{sin}\:{B}\:\mathrm{sin}\:{C}} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{4}\:\mathrm{cos}\:\frac{{A}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{cos}\:\frac{{C}}{\mathrm{2}}}{\mathrm{16}\:\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\mathrm{cos}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\mathrm{cos}\:\frac{{C}}{\mathrm{2}}\:} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}}{\mathrm{4}\:\:\mathrm{sin}\:\frac{{A}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{B}}{\mathrm{2}}\:\mathrm{sin}\:\frac{{C}}{\mathrm{2}}\:} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}}{\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}−\mathrm{1}\:} \\ $$$$\frac{{R}}{{r}}=\frac{\mathrm{1}}{\frac{\mathrm{5}}{\mathrm{4}}−\mathrm{1}\:}=\mathrm{4}\:\checkmark \\ $$
Commented by MJS_new last updated on 01/Jun/22

$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{such}\:\mathrm{triangle} \\ $$
Commented by mr W last updated on 01/Jun/22
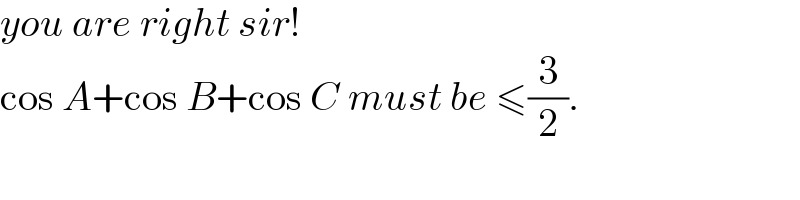
$${you}\:{are}\:{right}\:{sir}! \\ $$$$\mathrm{cos}\:{A}+\mathrm{cos}\:{B}+\mathrm{cos}\:{C}\:{must}\:{be}\:\leqslant\frac{\mathrm{3}}{\mathrm{2}}. \\ $$
Commented by mnjuly1970 last updated on 02/Jun/22

$$\:\:{thanks}\:\:{alot}… \\ $$
