Question Number 173983 by mnjuly1970 last updated on 23/Jul/22
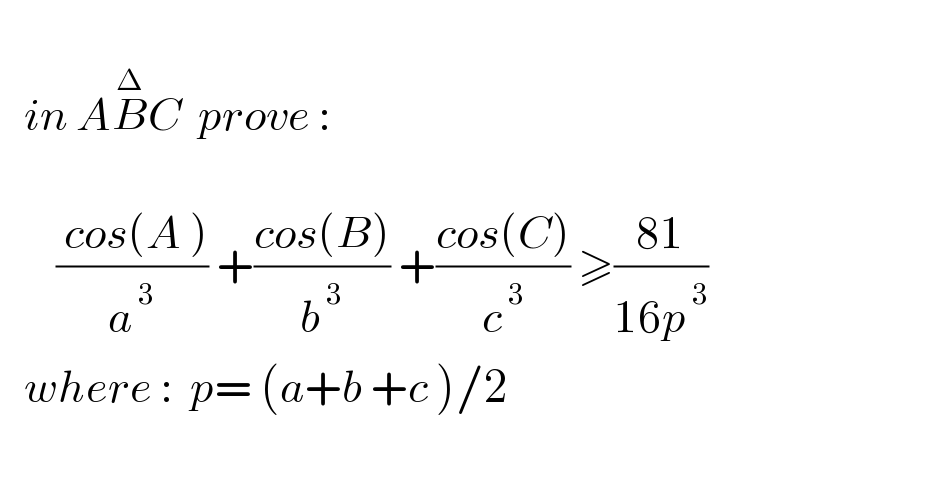
$$ \\ $$$$\:\:\:{in}\:{A}\overset{\Delta} {{B}C}\:\:{prove}\:: \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\frac{\:{cos}\left({A}\:\right)}{{a}^{\:\mathrm{3}} }\:+\frac{{cos}\left({B}\right)}{{b}^{\:\mathrm{3}} }\:+\frac{{cos}\left({C}\right)}{{c}^{\:\mathrm{3}} }\:\geqslant\frac{\mathrm{81}}{\mathrm{16}{p}^{\:\mathrm{3}} } \\ $$$$\:\:\:{where}\::\:\:{p}=\:\left({a}+{b}\:+{c}\:\right)/\mathrm{2} \\ $$$$ \\ $$
Answered by mnjuly1970 last updated on 23/Jul/22

$$\:\:{proof}\:: \\ $$$$\:\:{equivalently}\:{we}\:{must}\:{prove}: \\ $$$$\:\:\:\:\frac{{cos}\left({A}\right)}{{sin}^{\:\mathrm{3}} \left({A}\right)}\:+\frac{{cos}\left({B}\right)}{{sin}^{\:\mathrm{3}} \left({B}\right)}\:+\frac{{cos}\left({C}\right)}{{sin}^{\:\mathrm{3}} \left({C}\right)} \\ $$$$\:\:\:\:\:\geqslant\:\frac{\mathrm{81}}{\mathrm{2}\:\left\{\left({sin}\left({A}\right)+{sin}\left({B}\right)+{sin}\left({c}\right)\right)^{\mathrm{3}} \overset{?} {\geqslant}\mathrm{27}{sin}\left({A}\right){sin}\left({B}\right){sin}\left({C}\right)\right\}} \\ $$$$\:\:\:\:{also} \\ $$$$\:\:\:\frac{{cos}\left({A}\right).{sin}\left({B}\right).{sin}\left({C}\right)}{{sin}^{\:\mathrm{2}} \left({A}\right)}\:+ \\ $$$$\:\:\:\:\frac{{cos}\left({B}\right).{sin}\left({A}\right).{sin}\left({C}\right)}{{sin}^{\:\mathrm{2}} \left({B}\right)}\:+ \\ $$$$\:\:\:\:\frac{\:{cos}\left({C}\right).{sin}\left({A}\right).{sin}\left({B}\right)}{{sin}^{\:\mathrm{2}} \left({C}\right)}\:\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:{equivalently}: \\ $$$$\:\:\:\:\frac{{cos}\left({A}\right).{bc}}{{a}^{\:\mathrm{2}} }\:+\frac{{cos}\left({B}\right).{ac}}{{b}^{\:\mathrm{2}} }+\frac{{cos}\left({C}\right).{ab}}{{c}^{\:\mathrm{2}} }\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\: \\ $$$$\:\:\:{also} \\ $$$$\:\:\:\:\frac{{b}^{\:\mathrm{2}} +{c}^{\:\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{a}^{\:\mathrm{2}} }\:+\frac{{a}^{\:\mathrm{2}} +{c}^{\:\mathrm{2}} −{b}^{\:\mathrm{2}} }{\mathrm{2}{b}^{\:\mathrm{2}} }+\frac{{a}^{\:\mathrm{2}} +{b}^{\:\mathrm{2}} −{c}^{\:\mathrm{2}} }{\mathrm{2}{c}^{\:\mathrm{2}} }\geqslant\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\:\:\:\:{equivalently}: \\ $$$$\:\:\:\ast\left\{\:\frac{{b}^{\:\mathrm{2}} +{c}^{\:\mathrm{2}} }{{a}^{\:\mathrm{2}} }\:+\frac{{a}^{\:\mathrm{2}} +{c}^{\:\mathrm{2}} }{{b}^{\:\mathrm{2}} }\:+\frac{{a}^{\:\mathrm{2}} +{b}^{\:\mathrm{2}} }{{c}^{\:\mathrm{2}} }\right\}\:\overset{?} {\geqslant}\mathrm{6} \\ $$$$\:\:\:\ast\:{L}.{h}.{s}\:\overset{\boldsymbol{{am}}−\boldsymbol{{gm}}} {\geqslant}\:\left(\mathrm{2}\sqrt{\frac{{a}^{\:\mathrm{2}} }{{b}^{\:\mathrm{2}} }\:.\frac{{b}^{\:\mathrm{2}} }{{a}^{\:\mathrm{2}} }}\:+\mathrm{2}\sqrt{\frac{{a}^{\:\mathrm{2}} }{{c}^{\:\mathrm{2}} }.\frac{{c}^{\:\mathrm{2}} }{{a}^{\:\mathrm{2}} }}\:+\mathrm{2}\sqrt{\left.\frac{{b}^{\:\mathrm{2}} }{{c}^{\:\mathrm{2}} }.\frac{{c}^{\:\mathrm{2}} }{{b}\:\mathrm{2}}\:\right)}\right. \\ $$$$\:\:\:\:\:\:\:\:{L}.{h}.{s}\:\geqslant\:\mathrm{6}\:\:\blacksquare \\ $$$$\:\:\:\:\: \\ $$$$\:\:\: \\ $$
