Question Number 113667 by ZiYangLee last updated on 14/Sep/20
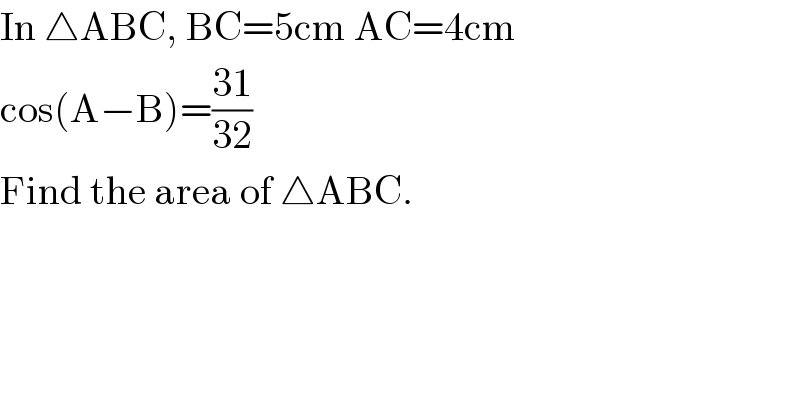
$$\mathrm{In}\:\bigtriangleup\mathrm{ABC},\:\mathrm{BC}=\mathrm{5cm}\:\mathrm{AC}=\mathrm{4cm} \\ $$$$\mathrm{cos}\left(\mathrm{A}−\mathrm{B}\right)=\frac{\mathrm{31}}{\mathrm{32}}\:\: \\ $$$$\mathrm{Find}\:\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\bigtriangleup\mathrm{ABC}. \\ $$
Answered by som(math1967) last updated on 14/Sep/20

$$\mathrm{tan}^{\mathrm{2}} \frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}=\frac{\mathrm{1}−\mathrm{cos}\left(\mathrm{A}−\mathrm{B}\right)}{\mathrm{1}+\mathrm{cos}\left(\mathrm{A}−\mathrm{B}\right)} \\ $$$$\mathrm{tan}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}=\sqrt{\frac{\mathrm{1}}{\mathrm{63}}}=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{7}}} \\ $$$$\:\frac{\mathrm{5}−\mathrm{4}}{\mathrm{5}+\mathrm{4}}×\mathrm{cot}\frac{\mathrm{C}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}\sqrt{\mathrm{7}}}\:\bigstar \\ $$$$\mathrm{cot}\frac{\mathrm{C}}{\mathrm{2}}=\frac{\mathrm{3}}{\:\sqrt{\mathrm{7}}} \\ $$$$\therefore\mathrm{sin}\frac{\mathrm{C}}{\mathrm{2}}=\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}\:,\mathrm{cos}\frac{\mathrm{C}}{\mathrm{2}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\therefore\mathrm{sinC}=\mathrm{2}×\frac{\sqrt{\mathrm{7}}}{\mathrm{4}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{3}\sqrt{\mathrm{7}}}{\mathrm{8}} \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{triangle} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{5}×\mathrm{4}×\frac{\mathrm{3}\sqrt{\mathrm{7}}}{\mathrm{8}} \\ $$$$\frac{\mathrm{15}\sqrt{\mathrm{7}}}{\mathrm{4}}\mathrm{cm}^{\mathrm{2}} \\ $$$$\bigstar\mathrm{tan}\frac{\mathrm{A}−\mathrm{B}}{\mathrm{2}}=\frac{\mathrm{a}−\mathrm{b}}{\mathrm{a}+\mathrm{b}}×\mathrm{cot}\frac{\mathrm{C}}{\mathrm{2}} \\ $$
Commented by ZiYangLee last updated on 16/Sep/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}\bigstar \\ $$
