Menu Close

In-an-arrangement-of-the-word-VIOLENT-find-the-chances-that-the-vowels-I-O-E-occupy-the-odd-positions-

Tinku Tara 0 Comments
Pin




Question Number 82130 by TawaTawa last updated on 18/Feb/20
In an arrangement of the word VIOLENT, find the chances that the vowels I, O, E occupy the odd positions.
$$\mathrm{In}\:\mathrm{an}\:\mathrm{arrangement}\:\mathrm{of}\:\mathrm{the}\:\mathrm{word}\:\:\mathrm{VIOLENT},\:\mathrm{find}\:\mathrm{the}\:\mathrm{chances} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{vowels}\:\:\:\mathrm{I},\:\mathrm{O},\:\mathrm{E}\:\:\:\mathrm{occupy}\:\mathrm{the}\:\mathrm{odd}\:\mathrm{positions}. \\ $$
Commented by mr W last updated on 18/Feb/20
we have 4 odd positions: 1, 3, 5, 7 we have 3 even positions: 2, 4, 6 we have 3 vowels: I, O, E we have 4 consonants: V, L, N, T assume we have 4 volwels: I, O, E, A. to arrange these 4 volwels in the 4 odd positions there are 4! ways. but the A is a fake, should be replaced with one of the 4 consonants, there are 4 possibilities. to arrange the 3 remaining consonants in the 3 even positions there are 3! ways. so we have totally 4!×4×3! ways to build words with volwels in odd positions.
$${we}\:{have}\:\mathrm{4}\:{odd}\:{positions}:\:\mathrm{1},\:\mathrm{3},\:\mathrm{5},\:\mathrm{7} \\ $$$${we}\:{have}\:\mathrm{3}\:{even}\:{positions}:\:\mathrm{2},\:\mathrm{4},\:\mathrm{6} \\ $$$${we}\:{have}\:\mathrm{3}\:{vowels}:\:{I},\:{O},\:{E}\: \\ $$$${we}\:{have}\:\mathrm{4}\:{consonants}:\:{V},\:{L},\:{N},\:{T} \\ $$$$ \\ $$$${assume}\:{we}\:{have}\:\mathrm{4}\:{volwels}:\:{I},\:{O},\:{E},\:{A}. \\ $$$${to}\:{arrange}\:{these}\:\mathrm{4}\:{volwels}\:{in}\:{the}\:\mathrm{4} \\ $$$${odd}\:{positions}\:{there}\:{are}\:\mathrm{4}!\:{ways}.\:{but} \\ $$$${the}\:{A}\:{is}\:{a}\:{fake},\:{should}\:{be}\:{replaced}\: \\ $$$${with}\:{one}\:{of}\:{the}\:\mathrm{4}\:{consonants},\:{there} \\ $$$${are}\:\mathrm{4}\:{possibilities}.\:{to}\:{arrange}\:{the} \\ $$$$\mathrm{3}\:{remaining}\:{consonants}\:{in}\:{the}\:\mathrm{3} \\ $$$${even}\:{positions}\:{there}\:{are}\:\mathrm{3}!\:{ways}.\:{so} \\ $$$${we}\:{have}\:{totally}\:\mathrm{4}!×\mathrm{4}×\mathrm{3}!\:{ways}\:{to} \\ $$$${build}\:{words}\:{with}\:{volwels}\:{in}\:{odd} \\ $$$${positions}. \\ $$
Commented by TawaTawa last updated on 19/Feb/20
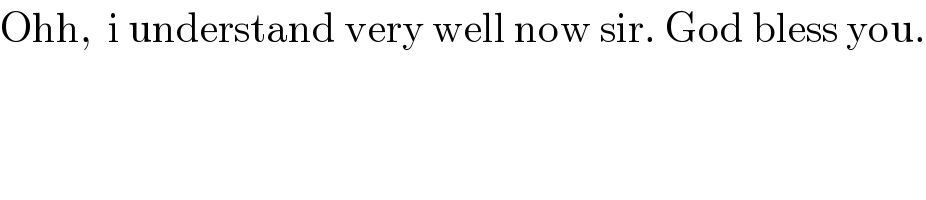
Ohh, i understand very well now sir. God bless you.
$$\mathrm{Ohh},\:\:\mathrm{i}\:\mathrm{understand}\:\mathrm{very}\:\mathrm{well}\:\mathrm{now}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
Commented by john santu last updated on 18/Feb/20
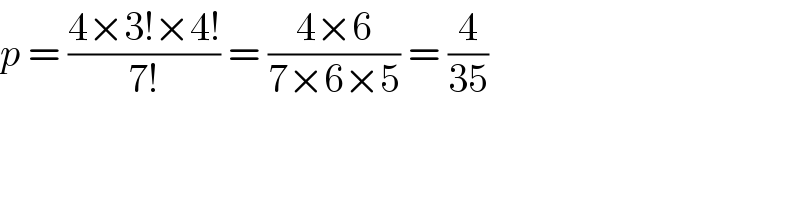
p = ((4×3!×4!)/(7!)) = ((4×6)/(7×6×5)) = (4/(35))
$${p}\:=\:\frac{\mathrm{4}×\mathrm{3}!×\mathrm{4}!}{\mathrm{7}!}\:=\:\frac{\mathrm{4}×\mathrm{6}}{\mathrm{7}×\mathrm{6}×\mathrm{5}}\:=\:\frac{\mathrm{4}}{\mathrm{35}} \\ $$
Commented by TawaTawa last updated on 18/Feb/20
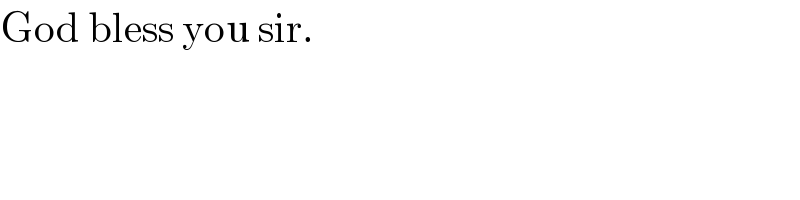
God bless you sir.
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Commented by TawaTawa last updated on 18/Feb/20
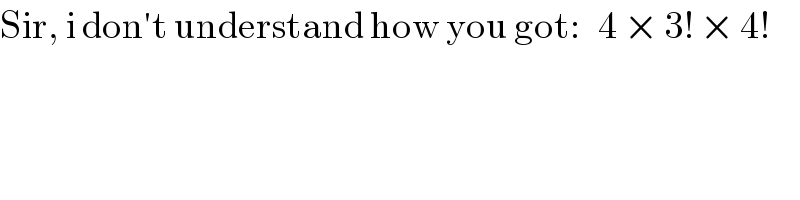
Sir, i don′t understand how you got: 4 × 3! × 4!
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{don}'\mathrm{t}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{you}\:\mathrm{got}:\:\:\:\mathrm{4}\:×\:\mathrm{3}!\:×\:\mathrm{4}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *