Menu Close

In-each-week-the-growth-of-a-plant-is-two-thirds-the-growth-of-the-previous-week-The-plant-grows-12-cm-in-the-first-week-a-Calculate-the-growth-of-the-plant-in-b-the-limiting-height-of-the-pant

Tinku Tara 0 Comments
Pin




Question Number 97483 by Rio Michael last updated on 08/Jun/20
In each week the growth of a plant is two−thirds the growth of the previous week. The plant grows 12 cm in the first week. (a) Calculate the growth of the plant in (b) the limiting height of the pant
$$\mathrm{In}\:\mathrm{each}\:\mathrm{week}\:\mathrm{the}\:\mathrm{growth}\:\mathrm{of}\:\mathrm{a}\:\mathrm{plant}\:\mathrm{is}\:\mathrm{two}−\mathrm{thirds} \\ $$$$\mathrm{the}\:\mathrm{growth}\:\mathrm{of}\:\mathrm{the}\:\mathrm{previous}\:\mathrm{week}. \\ $$$$\mathrm{The}\:\mathrm{plant}\:\mathrm{grows}\:\mathrm{12}\:\mathrm{cm}\:\mathrm{in}\:\mathrm{the}\:\mathrm{first}\:\mathrm{week}. \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{growth}\:\mathrm{of}\:\mathrm{the}\:\mathrm{plant}\:\mathrm{in}\: \\ $$$$\left(\mathrm{b}\right)\:\mathrm{the}\:\mathrm{limiting}\:\mathrm{height}\:\mathrm{of}\:\mathrm{the}\:\mathrm{pant} \\ $$
Commented by bobhans last updated on 08/Jun/20
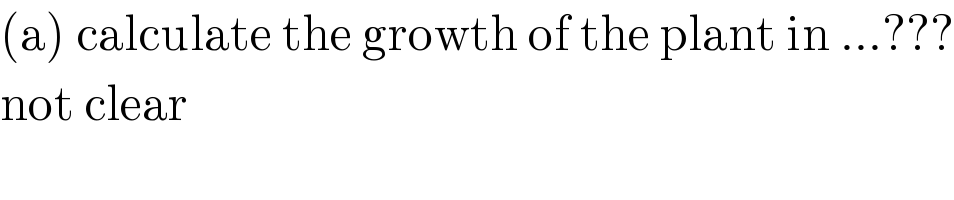
(a) calculate the growth of the plant in ...??? not clear
$$\left(\mathrm{a}\right)\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{growth}\:\mathrm{of}\:\mathrm{the}\:\mathrm{plant}\:\mathrm{in}\:…??? \\ $$$$\mathrm{not}\:\mathrm{clear} \\ $$
Commented by Rio Michael last updated on 08/Jun/20
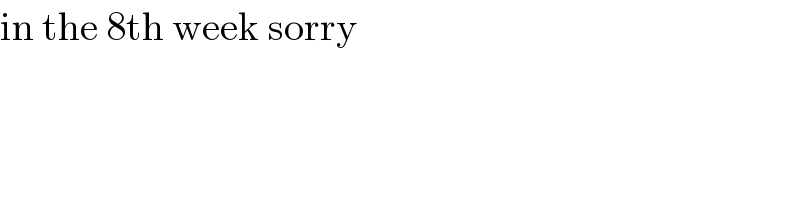
in the 8th week sorry
$$\mathrm{in}\:\mathrm{the}\:\mathrm{8th}\:\mathrm{week}\:\mathrm{sorry} \\ $$
Commented by bobhans last updated on 08/Jun/20
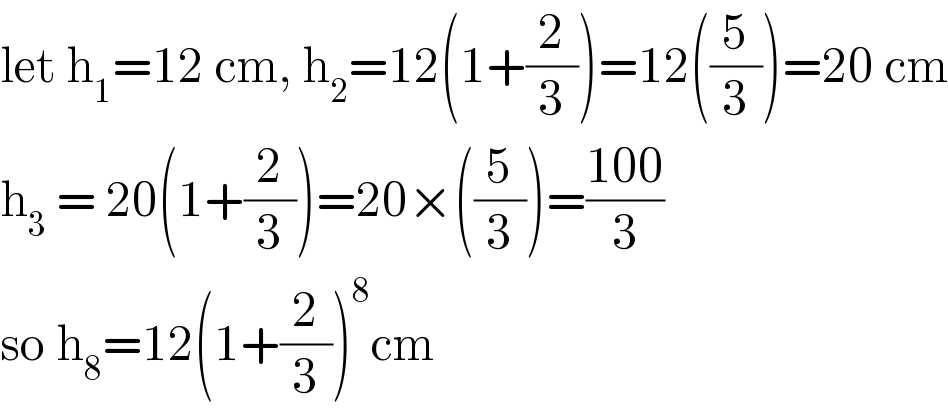
let h_1 =12 cm, h_2 =12(1+(2/3))=12((5/3))=20 cm h_3 = 20(1+(2/3))=20×((5/3))=((100)/3) so h_8 =12(1+(2/3))^8 cm
$$\mathrm{let}\:\mathrm{h}_{\mathrm{1}} =\mathrm{12}\:\mathrm{cm},\:\mathrm{h}_{\mathrm{2}} =\mathrm{12}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{12}\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=\mathrm{20}\:\mathrm{cm} \\ $$$$\mathrm{h}_{\mathrm{3}} \:=\:\mathrm{20}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)=\mathrm{20}×\left(\frac{\mathrm{5}}{\mathrm{3}}\right)=\frac{\mathrm{100}}{\mathrm{3}} \\ $$$$\mathrm{so}\:\mathrm{h}_{\mathrm{8}} =\mathrm{12}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{8}} \mathrm{cm} \\ $$
Commented by mr W last updated on 08/Jun/20
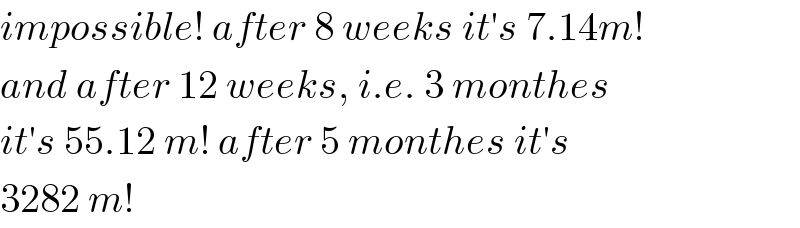
impossible! after 8 weeks it′s 7.14m! and after 12 weeks, i.e. 3 monthes it′s 55.12 m! after 5 monthes it′s 3282 m!
$${impossible}!\:{after}\:\mathrm{8}\:{weeks}\:{it}'{s}\:\mathrm{7}.\mathrm{14}{m}! \\ $$$${and}\:{after}\:\mathrm{12}\:{weeks},\:{i}.{e}.\:\mathrm{3}\:{monthes} \\ $$$${it}'{s}\:\mathrm{55}.\mathrm{12}\:{m}!\:{after}\:\mathrm{5}\:{monthes}\:{it}'{s} \\ $$$$\mathrm{3282}\:{m}! \\ $$
Answered by mr W last updated on 09/Jun/20
week 1: growth 12, height 12 week 2: growth 12×(2/3), height 12(1+(2/3)) week 3: growth 12×((2/3))^2 , height 12[1+(2/3)+((2/3))^2 ] ... week n: growth 12×((2/3))^(n−1) , height 12[1+(2/3)+((2/3))^2 +..+((2/3))^(n−1) ] height after n weeks: h_n =12[1+(2/3)+((2/3))^2 +..+((2/3))^(n−1) ]=((12[1−((2/3))^n ])/(1−(2/3))) ⇒h_n =36[1−((2/3))^n ] h_8 =36[1−((2/3))^8 ]=34.6 cm h_(max) =lim_(n→∞) h_n =36 cm
$${week}\:\mathrm{1}:\:{growth}\:\mathrm{12},\:{height}\:\mathrm{12} \\ $$$${week}\:\mathrm{2}:\:{growth}\:\mathrm{12}×\frac{\mathrm{2}}{\mathrm{3}},\:{height}\:\mathrm{12}\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$${week}\:\mathrm{3}:\:{growth}\:\mathrm{12}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} ,\:{height}\:\mathrm{12}\left[\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} \right] \\ $$$$… \\ $$$${week}\:{n}:\:{growth}\:\mathrm{12}×\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}−\mathrm{1}} ,\:{height}\:\mathrm{12}\left[\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +..+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}−\mathrm{1}} \right] \\ $$$${height}\:{after}\:{n}\:{weeks}:\:\:{h}_{{n}} =\mathrm{12}\left[\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} +..+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}−\mathrm{1}} \right]=\frac{\mathrm{12}\left[\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} \right]}{\mathrm{1}−\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$\Rightarrow{h}_{{n}} =\mathrm{36}\left[\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{n}} \right] \\ $$$${h}_{\mathrm{8}} =\mathrm{36}\left[\mathrm{1}−\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{8}} \right]=\mathrm{34}.\mathrm{6}\:{cm} \\ $$$$ \\ $$$${h}_{{max}} =\underset{{n}\rightarrow\infty} {\mathrm{lim}}{h}_{{n}} =\mathrm{36}\:{cm} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *