Question Number 105551 by mr W last updated on 29/Jul/20
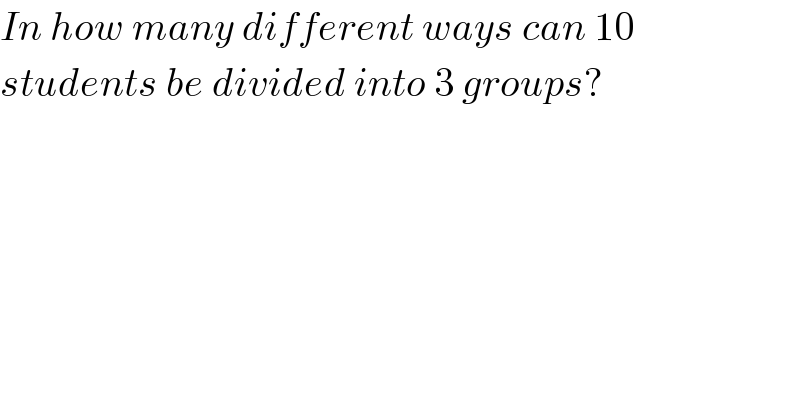
$${In}\:{how}\:{many}\:{different}\:{ways}\:{can}\:\mathrm{10} \\ $$$${students}\:{be}\:{divided}\:{into}\:\mathrm{3}\:{groups}? \\ $$
Answered by adhigenz last updated on 29/Jul/20

$$\mathrm{It}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same}\:\mathrm{thing}\:\mathrm{as}\:\mathrm{finding}\:\mathrm{how} \\ $$$$\mathrm{many}\:\mathrm{possible}\:\mathrm{integer}\:\mathrm{solution}\:\mathrm{for} \\ $$$$\mathrm{a}+\mathrm{b}+\mathrm{c}\:=\:\mathrm{10},\:\mathrm{which}\:\mathrm{a},\mathrm{b},\mathrm{c}\:\geqslant\:\mathrm{1},\:\mathrm{since}\:\mathrm{a} \\ $$$$\mathrm{certain}\:\mathrm{group}\:\mathrm{must}\:\mathrm{contain}\:\mathrm{at}\:\mathrm{least}\:\mathrm{1} \\ $$$$\mathrm{student}. \\ $$$$\mathrm{Let}\:{x}\:=\:{a}−\mathrm{1},\:{y}\:=\:{b}−\mathrm{1},\:{z}\:=\:{c}−\mathrm{1} \\ $$$$\mathrm{We}\:\mathrm{write}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{as}: \\ $$$${x}+{y}+{z}\:=\:\mathrm{7},\:\mathrm{for}\:{x},{y},{z}\:\geqslant\:\mathrm{0} \\ $$$$\mathrm{The}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{integer}\:\mathrm{is}\:\begin{pmatrix}{{n}+{r}−\mathrm{1}}\\{\:\:\:\:{r}−\mathrm{1}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{\mathrm{7}+\mathrm{3}−\mathrm{1}}\\{\:\:\:\:\mathrm{3}−\mathrm{1}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{\mathrm{9}}\\{\mathrm{2}}\end{pmatrix} \\ $$$$=\:\mathrm{36}\:\mathrm{ways} \\ $$
Commented by mr W last updated on 30/Jul/20

$${i}\:{don}'{t}\:{think}\:{both}\:{are}\:{the}\:{same}\:{thing}. \\ $$$$\mathrm{10}\:{students}\:{are}\:{distinct},\:{say}\:{they}\:{are} \\ $$$${A},{B},{C},{D},{E},{F},{G},{H},{I},{J}. \\ $$$${so}\:{for}\:{example} \\ $$$${A},{B},{C},{D}/{E},{F},{G}/{H},{I},{J} \\ $$$${and} \\ $$$${A},{B},{C},{E}/{D},{F},{G}/{H},{I},{J} \\ $$$${are}\:{two}\:{different}\:{ways}. \\ $$
Answered by 1549442205PVT last updated on 30/Jul/20

$$ \\ $$$$\mathrm{Consider}\:\mathrm{a}\:\mathrm{way}\:\mathrm{of}\:\mathrm{division}\:\mathrm{into}\:\mathrm{3}\:\mathrm{groups} \\ $$$$\mathrm{such}\:\mathrm{that}:\mathrm{one}\:\mathrm{group}\:\mathrm{of}\:\mathrm{two},\mathrm{one}\:\mathrm{group} \\ $$$$\mathrm{of}\:\mathrm{two}\:,\mathrm{one}\:\mathrm{group}\:\mathrm{of}\:\mathrm{six}.\mathrm{Since}\:\mathrm{for}\:\mathrm{first} \\ $$$$\mathrm{two}\:\mathrm{persons}\:\mathrm{we}\:\mathrm{have}\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{2}} \:\mathrm{ways}\:\mathrm{to}\:\mathrm{choose}, \\ $$$$\mathrm{for}\:\mathrm{next}\:\mathrm{two}\:\mathrm{persons}\:\mathrm{have}\:\mathrm{C}_{\mathrm{8}} ^{\mathrm{2}} \:\mathrm{ways}\:\mathrm{to}\: \\ $$$$\mathrm{choose}\:\mathrm{but}\:\mathrm{because}\:\mathrm{two}\:−\mathrm{person}\:\mathrm{repeated} \\ $$$$.\mathrm{Hence}\:\mathrm{all}\:\mathrm{have}\:\frac{\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{2}} ×\mathrm{C}_{\mathrm{8}} ^{\mathrm{2}} }{\mathrm{2}}=\mathrm{45}×\mathrm{14}=\mathrm{530} \\ $$$$\:\mathrm{ways}.\mathrm{Similarly},\mathrm{for}\:\mathrm{way}\:\mathrm{of}\:\mathrm{division} \\ $$$$\left(\mathrm{2},\mathrm{3},\mathrm{5}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{2}} ×\mathrm{C}_{\mathrm{8}} ^{\mathrm{3}} =\mathrm{45}×\mathrm{56}=\mathrm{2520}\:\mathrm{ways} \\ $$$$\left.\mathrm{iii}\right)\mathrm{For}\:\left(\mathrm{2},\mathrm{4},\mathrm{4}\right)\mathrm{have}\:\frac{\mathrm{C}_{\mathrm{10}} ^{\mathrm{2}} ×\mathrm{C}_{\mathrm{8}} ^{\mathrm{4}} }{\mathrm{2}}=\mathrm{45}.\mathrm{35}=\mathrm{1575} \\ $$$$\left.\mathrm{iv}\right)\mathrm{For}\:\left(\mathrm{3},\mathrm{3},\mathrm{4}\right)\mathrm{have}\:\frac{\mathrm{C}_{\mathrm{10}} ^{\mathrm{3}} ×\mathrm{C}_{\mathrm{7}} ^{\mathrm{3}} }{\mathrm{2}}=\mathrm{60}.\mathrm{35}=\mathrm{2100} \\ $$$$\mathrm{Thus},\mathrm{total}\:\mathrm{we}\:\mathrm{have}\:\mathrm{530}+\mathrm{2520}+\mathrm{1575}+\mathrm{2100} \\ $$$$=\mathrm{6725}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{divide}\:\mathrm{10}\:\mathrm{student}\:\mathrm{into} \\ $$$$\mathrm{three}\:\mathrm{groups}. \\ $$
Commented by mr W last updated on 30/Jul/20
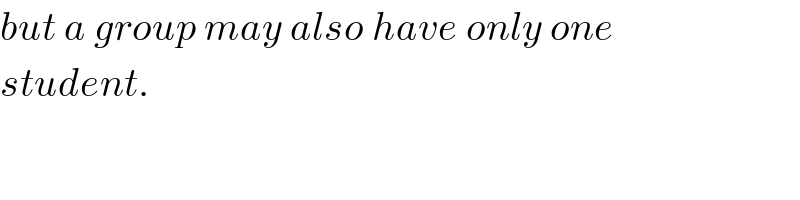
$${but}\:{a}\:{group}\:{may}\:{also}\:{have}\:{only}\:{one} \\ $$$${student}. \\ $$
Commented by 1549442205PVT last updated on 30/Jul/20
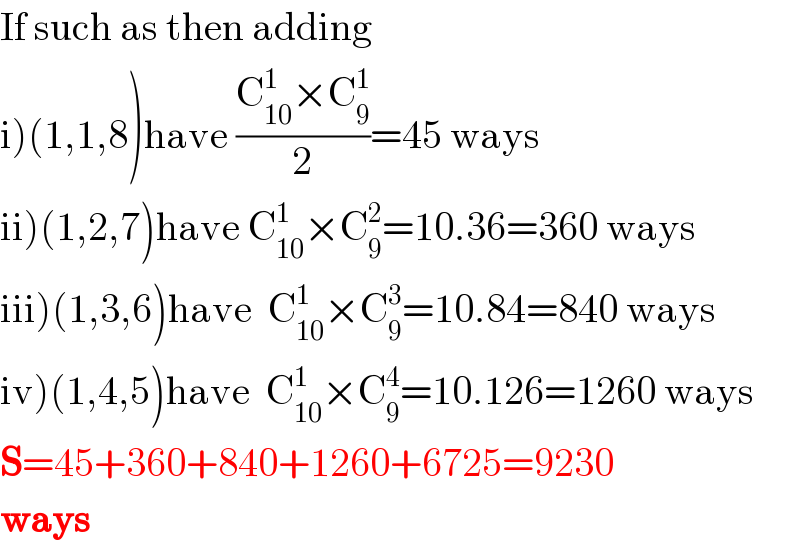
$$\mathrm{If}\:\mathrm{such}\:\mathrm{as}\:\mathrm{then}\:\mathrm{adding} \\ $$$$\left.\mathrm{i}\right)\left(\mathrm{1},\mathrm{1},\mathrm{8}\right)\mathrm{have}\:\frac{\mathrm{C}_{\mathrm{10}} ^{\mathrm{1}} ×\mathrm{C}_{\mathrm{9}} ^{\mathrm{1}} }{\mathrm{2}}=\mathrm{45}\:\mathrm{ways} \\ $$$$\left.\mathrm{ii}\right)\left(\mathrm{1},\mathrm{2},\mathrm{7}\right)\mathrm{have}\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{1}} ×\mathrm{C}_{\mathrm{9}} ^{\mathrm{2}} =\mathrm{10}.\mathrm{36}=\mathrm{360}\:\mathrm{ways} \\ $$$$\left.\mathrm{iii}\right)\left(\mathrm{1},\mathrm{3},\mathrm{6}\right)\mathrm{have}\:\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{1}} ×\mathrm{C}_{\mathrm{9}} ^{\mathrm{3}} =\mathrm{10}.\mathrm{84}=\mathrm{840}\:\mathrm{ways} \\ $$$$\left.\mathrm{iv}\right)\left(\mathrm{1},\mathrm{4},\mathrm{5}\right)\mathrm{have}\:\:\mathrm{C}_{\mathrm{10}} ^{\mathrm{1}} ×\mathrm{C}_{\mathrm{9}} ^{\mathrm{4}} =\mathrm{10}.\mathrm{126}=\mathrm{1260}\:\mathrm{ways} \\ $$$$\boldsymbol{\mathrm{S}}=\mathrm{45}+\mathrm{360}+\mathrm{840}+\mathrm{1260}+\mathrm{6725}=\mathrm{9230} \\ $$$$\boldsymbol{\mathrm{ways}} \\ $$
Commented by mr W last updated on 30/Jul/20

$${typo}\:{in}\:{result}\:{for}\:\left(\mathrm{2},\mathrm{2},\mathrm{6}\right):\:\mathrm{45}×\mathrm{14}=\mathrm{630} \\ $$$${instead}\:{of}\:\mathrm{530}!\: \\ $$$${then}\:{you}\:{get}\:{S}=\mathrm{9330} \\ $$$${this}\:{is}\:{correct},\:{nice}\:{work}\:{sir}! \\ $$
Commented by mr W last updated on 30/Jul/20

$${the}\:{coefficient}\:{of}\:{x}^{\mathrm{10}} \:{term}\:{from} \\ $$$${generating}\:{function} \\ $$$$\frac{\mathrm{10}!}{\mathrm{3}!}\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{3}} \:{is}\:\mathrm{9330}. \\ $$
Commented by mr W last updated on 30/Jul/20

Commented by 1549442205PVT last updated on 30/Jul/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{Sir}!\mathrm{You}\:\mathrm{are}\:\mathrm{welcome}. \\ $$
Commented by mr W last updated on 31/Jul/20

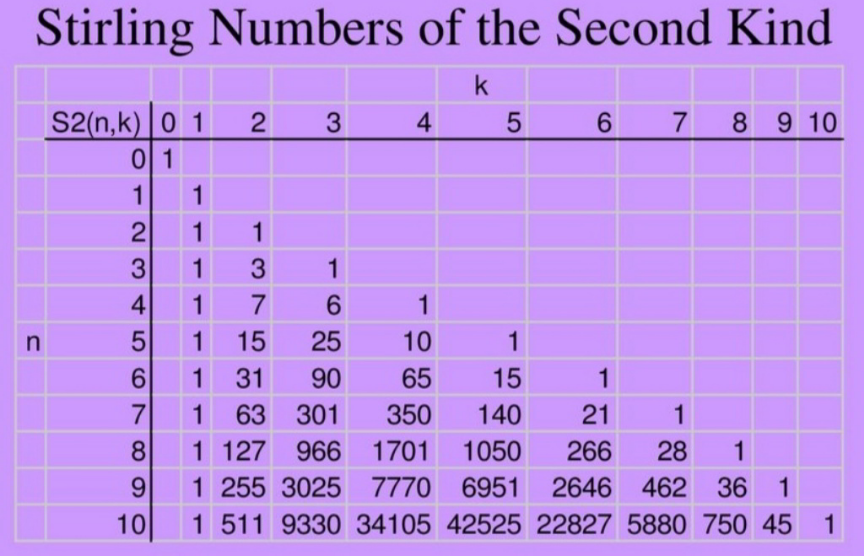
$${number}\:{of}\:{ways}\:{to}\:{place}\:{n}\:{distinct} \\ $$$${objects}\:{in}\:{k}\:{identical}\:{boxes}\:{is}\:\left\{_{{k}} ^{{n}} \right\} \\ $$$${which}\:{is}\:{the}\:{stirling}\:{number}\:{of}\:{the} \\ $$$${second}\:{kind}.\: \\ $$$$\left\{_{{k}} ^{{n}} \right\}={S}_{\mathrm{2}} \left({n},{k}\right) \\ $$$$\left\{_{\mathrm{3}} ^{\mathrm{10}} \right\}=\mathrm{9330}. \\ $$
Commented by mr W last updated on 31/Jul/20