Question Number 125191 by Don08q last updated on 08/Dec/20
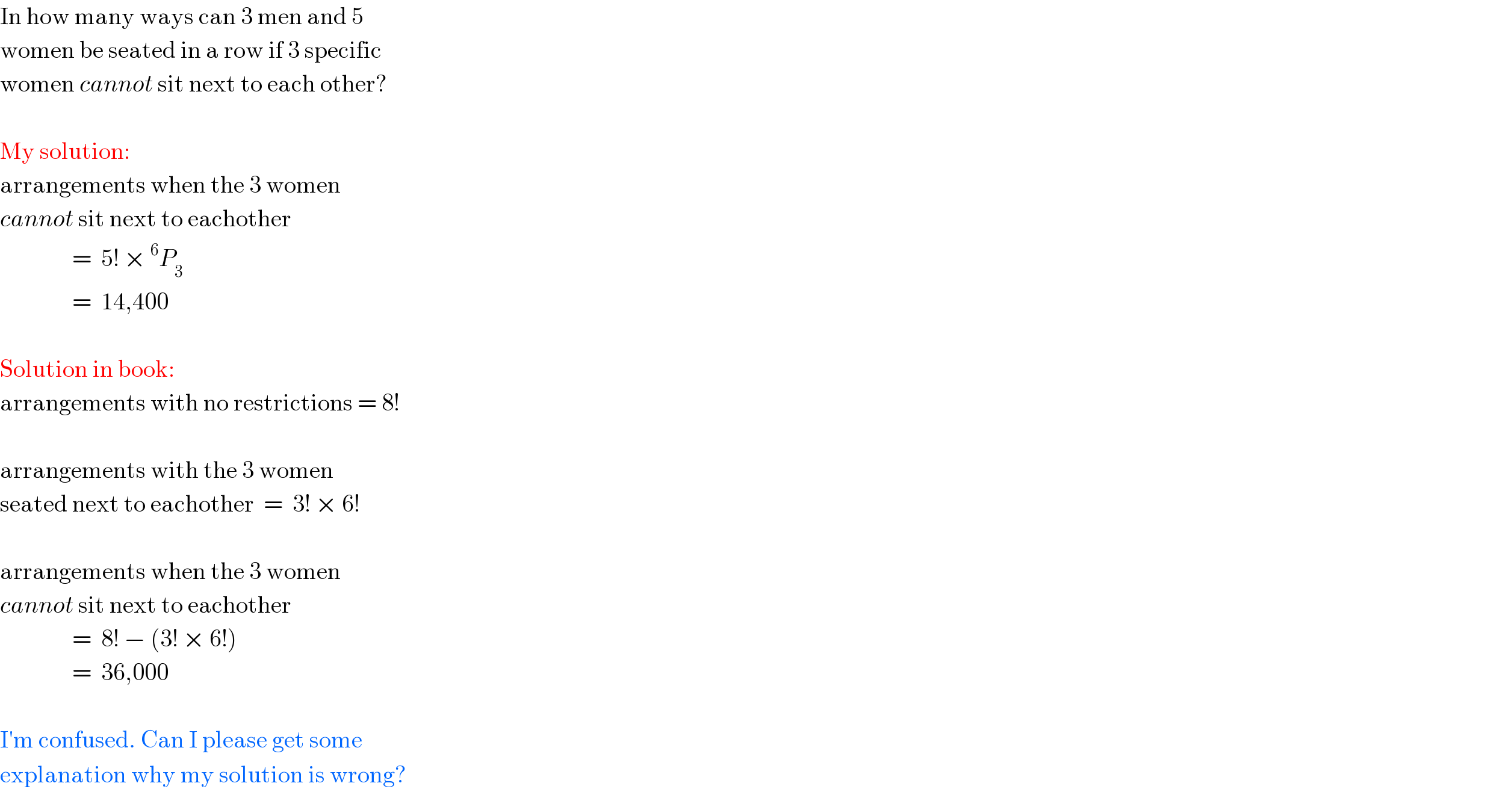
$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\mathrm{can}\:\mathrm{3}\:\mathrm{men}\:\mathrm{and}\:\mathrm{5} \\ $$$$\mathrm{women}\:\mathrm{be}\:\mathrm{seated}\:\mathrm{in}\:\mathrm{a}\:\mathrm{row}\:\mathrm{if}\:\mathrm{3}\:\mathrm{specific} \\ $$$$\mathrm{women}\:{cannot}\:\mathrm{sit}\:\mathrm{next}\:\mathrm{to}\:\mathrm{each}\:\mathrm{other}? \\ $$$$ \\ $$$$\mathrm{My}\:\mathrm{solution}: \\ $$$$\mathrm{arrangements}\:\mathrm{when}\:\mathrm{the}\:\mathrm{3}\:\mathrm{women} \\ $$$${cannot}\:\mathrm{sit}\:\mathrm{next}\:\mathrm{to}\:\mathrm{eachother}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{5}!\:×\:^{\mathrm{6}} {P}_{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{14},\mathrm{400} \\ $$$$ \\ $$$$\mathrm{Solution}\:\mathrm{in}\:\mathrm{book}: \\ $$$$\mathrm{arrangements}\:\mathrm{with}\:\mathrm{no}\:\mathrm{restrictions}\:=\:\mathrm{8}! \\ $$$$ \\ $$$$\mathrm{arrangements}\:\mathrm{with}\:\mathrm{the}\:\mathrm{3}\:\mathrm{women} \\ $$$$\mathrm{seated}\:\mathrm{next}\:\mathrm{to}\:\mathrm{eachother}\:\:=\:\:\mathrm{3}!\:×\:\mathrm{6}! \\ $$$$ \\ $$$$\mathrm{arrangements}\:\mathrm{when}\:\mathrm{the}\:\mathrm{3}\:\mathrm{women} \\ $$$${cannot}\:\mathrm{sit}\:\mathrm{next}\:\mathrm{to}\:\mathrm{eachother}\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{8}!\:−\:\left(\mathrm{3}!\:×\:\mathrm{6}!\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\mathrm{36},\mathrm{000} \\ $$$$ \\ $$$$\mathrm{I}'\mathrm{m}\:\mathrm{confused}.\:\mathrm{Can}\:\mathrm{I}\:\mathrm{please}\:\mathrm{get}\:\mathrm{some} \\ $$$$\mathrm{explanation}\:\mathrm{why}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{wrong}? \\ $$
Commented by liberty last updated on 09/Dec/20
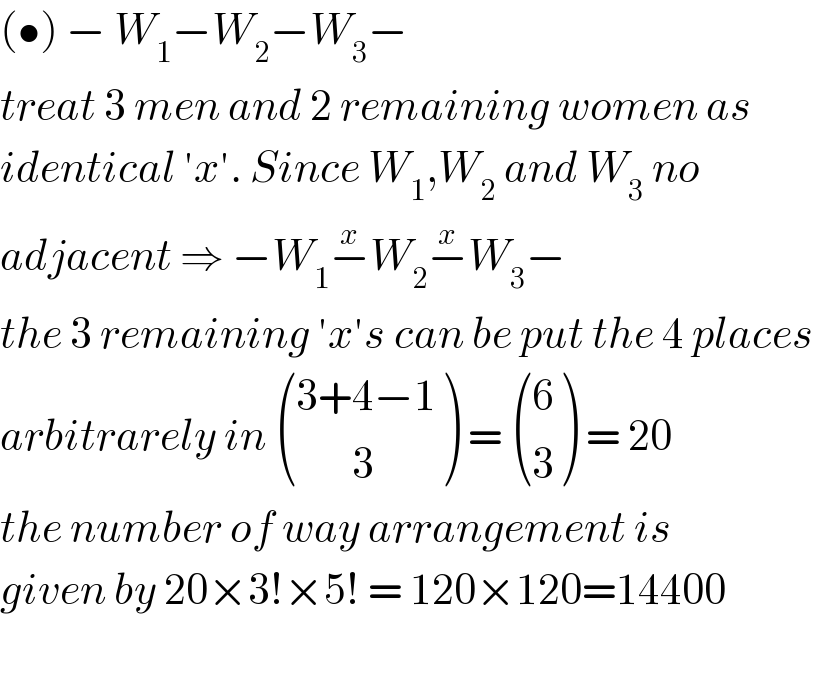
$$\left(\bullet\right)\:−\:{W}_{\mathrm{1}} −{W}_{\mathrm{2}} −{W}_{\mathrm{3}} − \\ $$$${treat}\:\mathrm{3}\:{men}\:{and}\:\mathrm{2}\:{remaining}\:{women}\:{as} \\ $$$${identical}\:'{x}'.\:{Since}\:{W}_{\mathrm{1}} ,{W}_{\mathrm{2}} \:{and}\:{W}_{\mathrm{3}} \:{no}\: \\ $$$${adjacent}\:\Rightarrow\:−{W}_{\mathrm{1}} \overset{{x}} {−}{W}_{\mathrm{2}} \overset{{x}} {−}{W}_{\mathrm{3}} − \\ $$$${the}\:\mathrm{3}\:{remaining}\:'{x}'{s}\:{can}\:{be}\:{put}\:{the}\:\mathrm{4}\:{places} \\ $$$${arbitrarely}\:{in}\:\begin{pmatrix}{\mathrm{3}+\mathrm{4}−\mathrm{1}}\\{\:\:\:\:\:\:\:\mathrm{3}}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{6}}\\{\mathrm{3}}\end{pmatrix}\:=\:\mathrm{20} \\ $$$${the}\:{number}\:{of}\:{way}\:{arrangement}\:{is} \\ $$$${given}\:{by}\:\mathrm{20}×\mathrm{3}!×\mathrm{5}!\:=\:\mathrm{120}×\mathrm{120}=\mathrm{14400} \\ $$$$ \\ $$
Commented by mr W last updated on 09/Dec/20

$${both}\:{of}\:{you}\:{are}\:{wrong}\:{sirs}. \\ $$$${you}\:{treated}\:{the}\:{cases}\:{that}\:“{no}\:{two}\:{of} \\ $$$${the}\:{three}\:{women}\:{are}\:{next}\:{to}\:{each} \\ $$$${other}''.\:{but}\:{the}\:{question}\:{askes}\:{that} \\ $$$$“{all}\:{the}\:{three}\:{women}\:{are}\:{not}\:{next} \\ $$$${to}\:{each}\:{other}''.\:{that}\:{means}\:{according} \\ $$$${to}\:{the}\:{question}\:{we}\:{should}\:{only}\:{exclude} \\ $$$${the}\:{cases}\:{that}\:{all}\:{the}\:{three}\:{women} \\ $$$${are}\:{together}.\:{but}\:{in}\:{your}\:{solutions} \\ $$$${you}\:{exclude}\:{also}\:{the}\:{cases}\:{that}\:{two} \\ $$$${of}\:{the}\:{three}\:{women}\:{are}\:{together}. \\ $$$${the}\:{solution}\:{given}\:{in}\:{book}\:{is}\:{correct}. \\ $$
Commented by mr W last updated on 09/Dec/20

$${again}:\:{according}\:{to}\:{question}\:{it}\:{is} \\ $$$${allowed}\:{when}\:{two}\:{of}\:{the}\:{three}\:{women} \\ $$$${are}\:{together}.\:{but}\:{this}\:{is}\:{not}\:{allowed} \\ $$$${in}\:{your}\:{solutions}. \\ $$
Commented by liberty last updated on 11/Dec/20

$${yeah}….{i}\:{misunderstanding}\:{the}\:{question}. \\ $$
