Question Number 124712 by benjo_mathlover last updated on 05/Dec/20
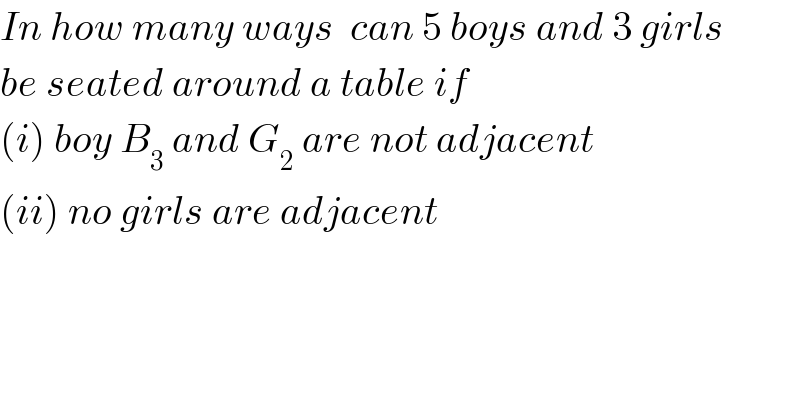
$${In}\:{how}\:{many}\:{ways}\:\:{can}\:\mathrm{5}\:{boys}\:{and}\:\mathrm{3}\:{girls} \\ $$$${be}\:{seated}\:{around}\:{a}\:{table}\:{if}\: \\ $$$$\left({i}\right)\:{boy}\:{B}_{\mathrm{3}} \:{and}\:{G}_{\mathrm{2}} \:{are}\:{not}\:{adjacent} \\ $$$$\left({ii}\right)\:{no}\:{girls}\:{are}\:{adjacent}\: \\ $$
Answered by liberty last updated on 05/Dec/20

$$\left({i}\right)\:{The}\:\mathrm{5}\:{boys}\:{and}\:\mathrm{2}\:{girls}\:{not}\:{including} \\ $$$$\:{G}_{\mathrm{2}} \:{can}\:{be}\:{seated}\:\left(\mathrm{7}−\mathrm{1}\right)!\:{ways}.\:{G}_{\mathrm{2}} \:{has}\:\left(\mathrm{7}−\mathrm{2}\right) \\ $$$${choices}\:{for}\:{a}\:{set}\:{not}\:{adjacent}\:{to}\:{B}_{\mathrm{3}} .\:{Thus} \\ $$$${the}\:{desired}\:{number}\:{ways}\:{is}\:\mathrm{6}!×\mathrm{5}=\mathrm{3600} \\ $$$${or}\:{the}\:{other}\:{method}\:{by}\:{Principle}\:{of}\: \\ $$$${Complementation}.\:{If}\:{A}\:{is}\:{a}\:{subset}\:{of}\:{a} \\ $$$${finite}\:{universal}\:{set}\:\mathcal{U}\:{then}\:\mid\mathcal{U}\:\backslash\:{A}\:\mid\:=\:\mid\mathcal{U}\mid−\mid{A}\mid \\ $$$${Now}\:{the}\:{number}\:{of}\:{ways}\:{to}\:{arrange}\:{the}\:\mathrm{5}\:{boys} \\ $$$${and}\:\mathrm{3}\:{girls}\:{around}\:{a}\:{table}\:{so}\:{that}\:{B}_{\mathrm{3}} \:{and} \\ $$$${G}_{\mathrm{2}} \:{are}\:{adjacent}\:\left\{{B}_{\mathrm{3}} ,{G}_{\mathrm{2}} \right\}\:{as}\:{an}\:{entity}\:{is} \\ $$$$\left(\mathrm{7}−\mathrm{1}\right)!×\mathrm{2}\:=\:\mathrm{1440} \\ $$$${Thus}\:{the}\:{desired}\:{number}\:{of}\:{ways}\:{is}\: \\ $$$$\left(\mathrm{8}−\mathrm{1}\right)!−\mathrm{1440}=\mathrm{3600} \\ $$
Commented by mr W last updated on 05/Dec/20

$${what}\:{did}\:{you}\:{get}\:{for}\:\left({ii}\right)? \\ $$
Commented by liberty last updated on 06/Dec/20
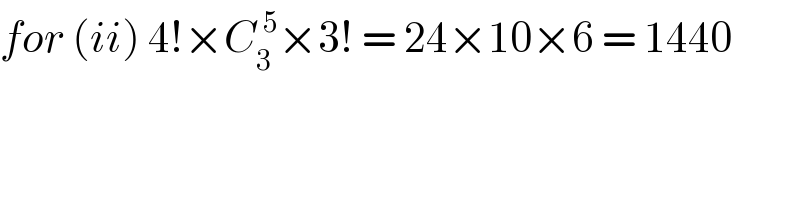
$${for}\:\left({ii}\right)\:\mathrm{4}!×{C}_{\mathrm{3}} ^{\:\mathrm{5}} ×\mathrm{3}!\:=\:\mathrm{24}×\mathrm{10}×\mathrm{6}\:=\:\mathrm{1440} \\ $$
Answered by mr W last updated on 06/Dec/20

$$\left({i}\right) \\ $$$$\mathrm{7}!−\mathrm{2}×\mathrm{6}!=\mathrm{3600} \\ $$$$\left({ii}\right) \\ $$$$\mathrm{4}!×{P}_{\mathrm{3}} ^{\mathrm{5}} =\mathrm{1440} \\ $$
Commented by benjo_mathlover last updated on 05/Dec/20
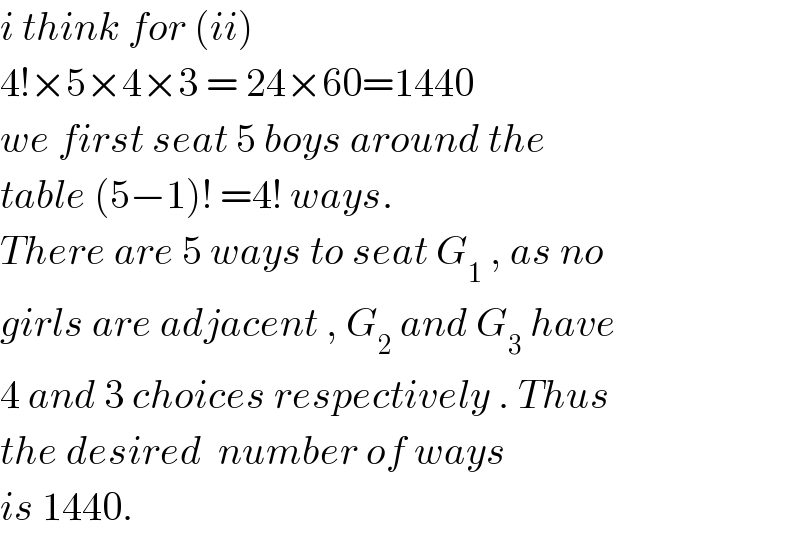
$${i}\:{think}\:{for}\:\left({ii}\right)\: \\ $$$$\mathrm{4}!×\mathrm{5}×\mathrm{4}×\mathrm{3}\:=\:\mathrm{24}×\mathrm{60}=\mathrm{1440} \\ $$$${we}\:{first}\:{seat}\:\mathrm{5}\:{boys}\:{around}\:{the}\: \\ $$$${table}\:\left(\mathrm{5}−\mathrm{1}\right)!\:=\mathrm{4}!\:{ways}. \\ $$$${There}\:{are}\:\mathrm{5}\:{ways}\:{to}\:{seat}\:{G}_{\mathrm{1}} \:,\:{as}\:{no} \\ $$$${girls}\:{are}\:{adjacent}\:,\:{G}_{\mathrm{2}} \:{and}\:{G}_{\mathrm{3}} \:{have} \\ $$$$\mathrm{4}\:{and}\:\mathrm{3}\:{choices}\:{respectively}\:.\:{Thus} \\ $$$${the}\:{desired}\:\:{number}\:{of}\:{ways} \\ $$$${is}\:\mathrm{1440}. \\ $$
Commented by liberty last updated on 06/Dec/20
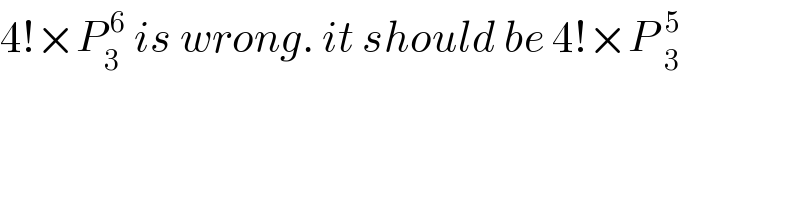
$$\mathrm{4}!×{P}_{\mathrm{3}} ^{\:\mathrm{6}} \:{is}\:{wrong}.\:{it}\:{should}\:{be}\:\mathrm{4}!×{P}\:_{\mathrm{3}} ^{\mathrm{5}} \\ $$
Commented by mr W last updated on 06/Dec/20
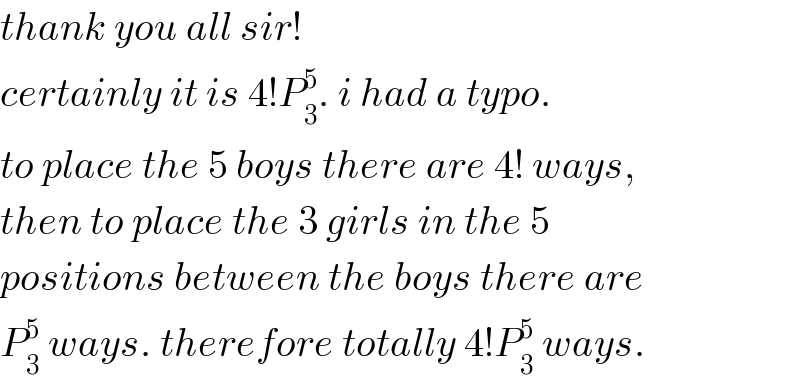
$${thank}\:{you}\:{all}\:{sir}! \\ $$$${certainly}\:{it}\:{is}\:\mathrm{4}!{P}_{\mathrm{3}} ^{\mathrm{5}} .\:{i}\:{had}\:{a}\:{typo}. \\ $$$${to}\:{place}\:{the}\:\mathrm{5}\:{boys}\:{there}\:{are}\:\mathrm{4}!\:{ways}, \\ $$$${then}\:{to}\:{place}\:{the}\:\mathrm{3}\:{girls}\:{in}\:{the}\:\mathrm{5}\: \\ $$$${positions}\:{between}\:{the}\:{boys}\:{there}\:{are} \\ $$$${P}_{\mathrm{3}} ^{\mathrm{5}} \:{ways}.\:{therefore}\:{totally}\:\mathrm{4}!{P}_{\mathrm{3}} ^{\mathrm{5}} \:{ways}. \\ $$
