Question Number 153572 by otchereabdullai@gmail.com last updated on 10/Sep/21
$$\mathrm{In}\:\mathrm{how}\:\mathrm{many}\:\mathrm{ways}\:\:\mathrm{can}\:\mathrm{6}\:\mathrm{players}\:\mathrm{be}\: \\ $$$$\mathrm{lined}\:\mathrm{up}\:\mathrm{if}\:\mathrm{2}\:\mathrm{particlar}\:\mathrm{players}\:\mathrm{must}\: \\ $$$$\mathrm{not}\:\mathrm{stand}\:\mathrm{next}\:\mathrm{to}\:\mathrm{each}\:\mathrm{other} \\ $$
Commented by Tawa11 last updated on 08/Sep/21
![Let the players be ABCDEF ⇒ ∗ C ∗ D ∗ E ∗ F ∗ [A and B are not next to each other] ∴ = 4! × 5 × 4 ∴ = 24 × 20 ∴ = 480 ways.](https://www.tinkutara.com/question/Q153606.png)
$$\mathrm{Let}\:\mathrm{the}\:\mathrm{players}\:\mathrm{be}\:\:\:\:\mathrm{ABCDEF} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\ast\:\:\:\mathrm{C}\:\:\:\ast\:\:\:\mathrm{D}\:\:\:\ast\:\:\:\:\:\mathrm{E}\:\:\:\ast\:\:\:\mathrm{F}\:\:\ast\:\:\:\:\:\:\:\:\:\:\left[\mathrm{A}\:\:\:\mathrm{and}\:\:\:\mathrm{B}\:\:\:\:\mathrm{are}\:\mathrm{not}\:\mathrm{next}\:\mathrm{to}\:\mathrm{each}\:\mathrm{other}\right] \\ $$$$\therefore\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\mathrm{4}!\:\:×\:\:\mathrm{5}\:\:×\:\:\mathrm{4} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\mathrm{24}\:\:×\:\:\mathrm{20} \\ $$$$\therefore\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\mathrm{480}\:\mathrm{ways}. \\ $$
Answered by mr W last updated on 08/Sep/21
$${XAYBX} \\ $$$${X}={zero}\:{or}\:{more}\:{players} \\ $$$${Y}={one}\:{or}\:{more}\:{players} \\ $$$$\mathrm{2}{X}+{Y}=\mathrm{4} \\ $$$$\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +…\right)^{\mathrm{2}} \left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +…\right) \\ $$$$=\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}+\mathrm{1}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{4}} \:{is}\:{C}_{\mathrm{2}} ^{\mathrm{3}+\mathrm{2}} ={C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{10}. \\ $$$${totally}\:{ways}: \\ $$$${C}_{\mathrm{2}} ^{\mathrm{5}} ×\mathrm{2}!×\mathrm{4}!=\mathrm{480} \\ $$
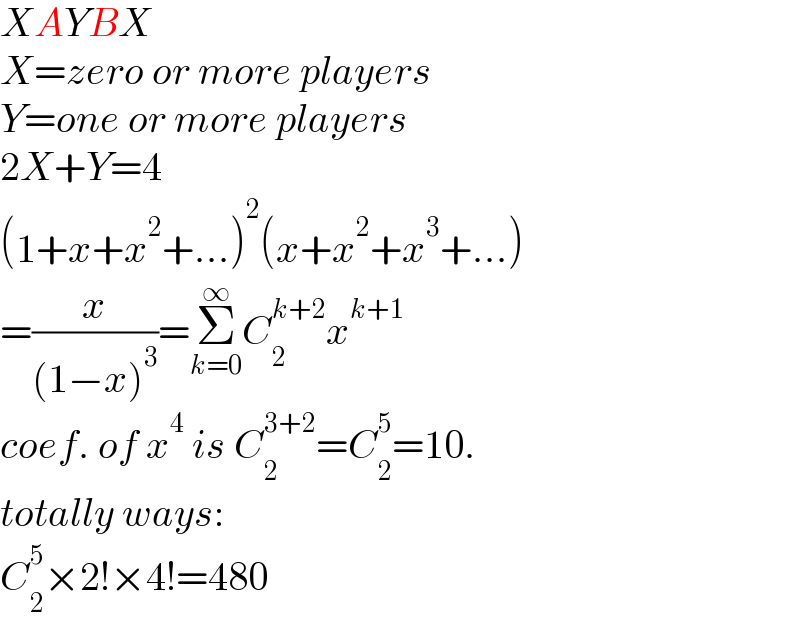
Commented by mr W last updated on 08/Sep/21
$${C}_{\mathrm{2}} ^{\mathrm{5}} =\mathrm{10}: \\ $$$${APBPPP} \\ $$$${APPPBP} \\ $$$${APPBPP} \\ $$$${APPPPB} \\ $$$${PAPBPP} \\ $$$${PAPPBP} \\ $$$${PAPPPB} \\ $$$${PPAPBP} \\ $$$${PPAPPB} \\ $$$${PPPAPB} \\ $$$$ \\ $$$${you}\:{can}\:{also}\:{line}\:{up}\:{the}\:{other}\:\mathrm{4}\:{players}, \\ $$$$\_{P\_P\_P\_P\_} \\ $$$${and}\:{then}\:{place}\:{the}\:{two}\:{particular} \\ $$$${players}\:{at}\:{the}\:{five}\:\_\:{positions},\:{like} \\ $$$$\_{PAP\_P\_PB}.\:{there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{5}} \: \\ $$$${possibilities}. \\ $$
Commented by otchereabdullai@gmail.com last updated on 08/Sep/21
$$\mathrm{may}\:\mathrm{God}\:\mathrm{continue}\:\mathrm{to}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{always} \\ $$$$\mathrm{prof}\:\mathrm{W} \\ $$
Answered by peter frank last updated on 08/Sep/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{both} \\ $$