Menu Close

In-the-expansion-1-1-2-x-n-the-coefficient-of-x-m-is-5-4-times-the-coefficient-of-x-m-1-a-Show-that-5n-13m-8-b-If-m-and-n-are-positive-integers-such-that-m-n-determine-the-smalles

Tinku Tara 0 Comments
Pin




Question Number 154225 by ZiYangLee last updated on 15/Sep/21
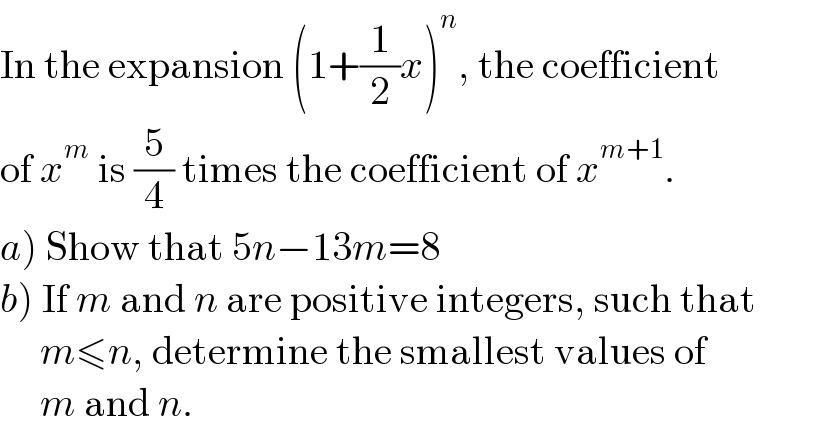
In the expansion (1+(1/2)x)^n , the coefficient of x^m is (5/4) times the coefficient of x^(m+1) . a) Show that 5n−13m=8 b) If m and n are positive integers, such that m≤n, determine the smallest values of m and n.
$$\mathrm{In}\:\mathrm{the}\:\mathrm{expansion}\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{{n}} ,\:\mathrm{the}\:\mathrm{coefficient} \\ $$$$\mathrm{of}\:{x}^{{m}} \:\mathrm{is}\:\frac{\mathrm{5}}{\mathrm{4}}\:\mathrm{times}\:\mathrm{the}\:\mathrm{coefficient}\:\mathrm{of}\:{x}^{{m}+\mathrm{1}} . \\ $$$$\left.{a}\right)\:\mathrm{Show}\:\mathrm{that}\:\mathrm{5}{n}−\mathrm{13}{m}=\mathrm{8} \\ $$$$\left.{b}\right)\:\mathrm{If}\:{m}\:\mathrm{and}\:{n}\:\mathrm{are}\:\mathrm{positive}\:\mathrm{integers},\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\:\:\:{m}\leqslant{n},\:\mathrm{determine}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{values}\:\mathrm{of} \\ $$$$\:\:\:\:\:{m}\:\mathrm{and}\:{n}. \\ $$
Commented by ZiYangLee last updated on 15/Sep/21
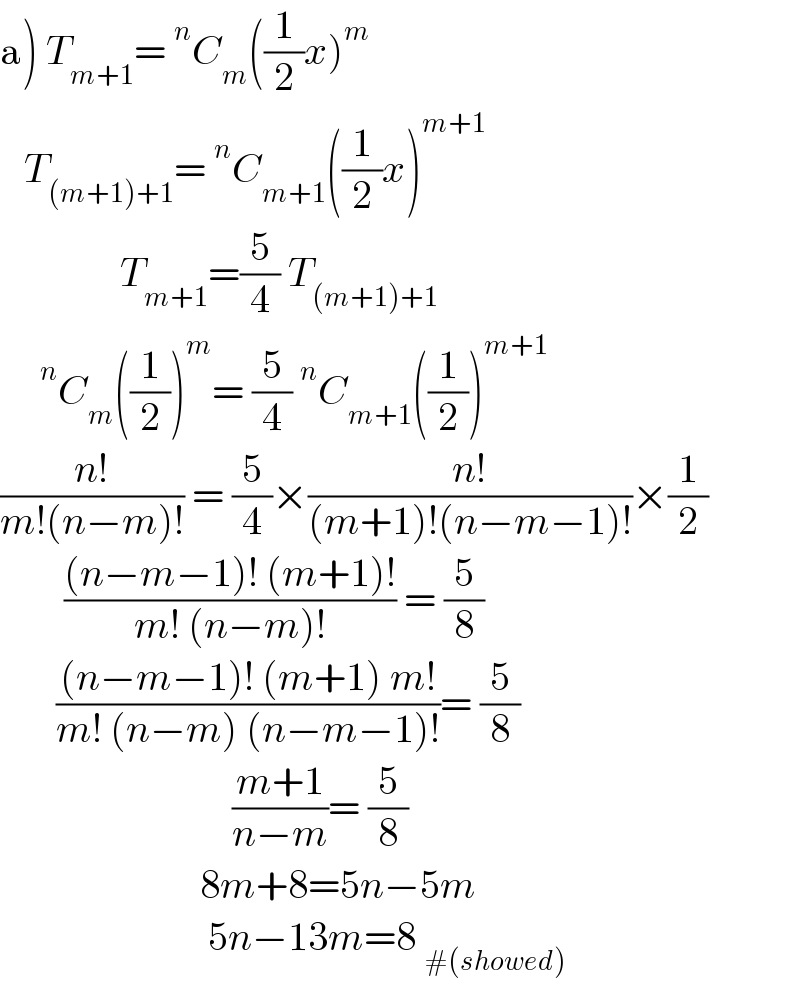
a) T_(m+1) =^n C_m ((1/2)x)^m T_((m+1)+1) =^n C_(m+1) ((1/2)x)^(m+1) T_(m+1) =(5/4) T_((m+1)+1) ^n C_m ((1/2))^m = (5/4)^n C_(m+1) ((1/2))^(m+1) ((n!)/(m!(n−m)!)) = (5/4)×((n!)/((m+1)!(n−m−1)!))×(1/2) (((n−m−1)! (m+1)!)/(m! (n−m)!)) = (5/8) (((n−m−1)! (m+1) m!)/(m! (n−m) (n−m−1)!))= (5/8) ((m+1)/(n−m))= (5/8) 8m+8=5n−5m 5n−13m=8 _(#(showed))
$$\left.\mathrm{a}\right)\:{T}_{{m}+\mathrm{1}} =\:^{{n}} {C}_{{m}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{{m}} \\ $$$$\:\:\:{T}_{\left({m}+\mathrm{1}\right)+\mathrm{1}} =\:^{{n}} {C}_{{m}+\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}{x}\right)^{{m}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{T}_{{m}+\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{4}}\:{T}_{\left({m}+\mathrm{1}\right)+\mathrm{1}} \\ $$$$\:\:\:\:\:^{{n}} {C}_{{m}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}} =\:\frac{\mathrm{5}}{\mathrm{4}}\:^{{n}} {C}_{{m}+\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{{m}+\mathrm{1}} \\ $$$$\frac{{n}!}{{m}!\left({n}−{m}\right)!}\:=\:\frac{\mathrm{5}}{\mathrm{4}}×\frac{{n}!}{\left({m}+\mathrm{1}\right)!\left({n}−{m}−\mathrm{1}\right)!}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\frac{\left({n}−{m}−\mathrm{1}\right)!\:\left({m}+\mathrm{1}\right)!}{{m}!\:\left({n}−{m}\right)!}\:=\:\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\frac{\left({n}−{m}−\mathrm{1}\right)!\:\left({m}+\mathrm{1}\right)\:{m}!}{{m}!\:\left({n}−{m}\right)\:\left({n}−{m}−\mathrm{1}\right)!}=\:\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{m}+\mathrm{1}}{{n}−{m}}=\:\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{8}{m}+\mathrm{8}=\mathrm{5}{n}−\mathrm{5}{m} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{5}{n}−\mathrm{13}{m}=\mathrm{8}\:_{#\left({showed}\right)} \\ $$
Answered by mr W last updated on 15/Sep/21
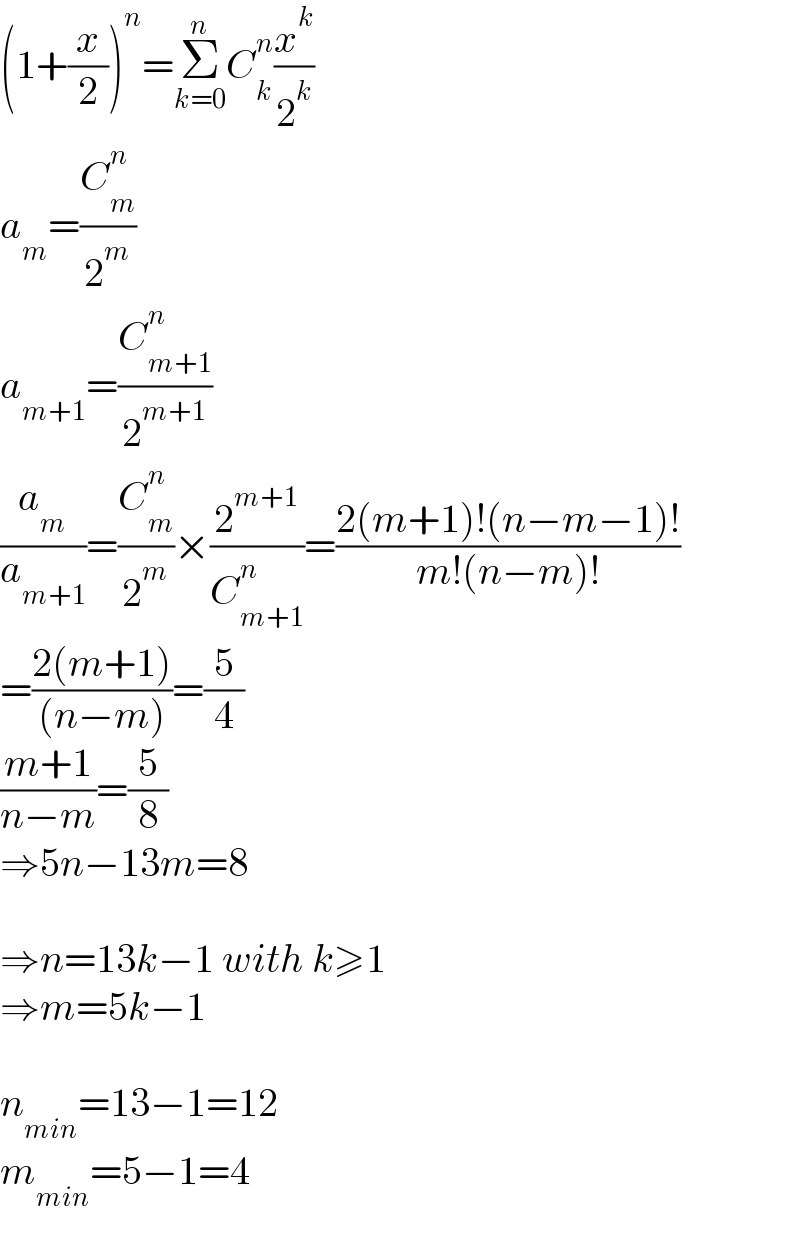
(1+(x/2))^n =Σ_(k=0) ^n C_k ^n (x^k /2^k ) a_m =(C_m ^n /2^m ) a_(m+1) =(C_(m+1) ^n /2^(m+1) ) (a_m /a_(m+1) )=(C_m ^n /2^m )×(2^(m+1) /C_(m+1) ^n )=((2(m+1)!(n−m−1)!)/(m!(n−m)!)) =((2(m+1))/((n−m)))=(5/4) ((m+1)/(n−m))=(5/8) ⇒5n−13m=8 ⇒n=13k−1 with k≥1 ⇒m=5k−1 n_(min) =13−1=12 m_(min) =5−1=4
$$\left(\mathrm{1}+\frac{{x}}{\mathrm{2}}\right)^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{C}_{{k}} ^{{n}} \frac{{x}^{{k}} }{\mathrm{2}^{{k}} } \\ $$$${a}_{{m}} =\frac{{C}_{{m}} ^{{n}} }{\mathrm{2}^{{m}} } \\ $$$${a}_{{m}+\mathrm{1}} =\frac{{C}_{{m}+\mathrm{1}} ^{{n}} }{\mathrm{2}^{{m}+\mathrm{1}} } \\ $$$$\frac{{a}_{{m}} }{{a}_{{m}+\mathrm{1}} }=\frac{{C}_{{m}} ^{{n}} }{\mathrm{2}^{{m}} }×\frac{\mathrm{2}^{{m}+\mathrm{1}} }{{C}_{{m}+\mathrm{1}} ^{{n}} }=\frac{\mathrm{2}\left({m}+\mathrm{1}\right)!\left({n}−{m}−\mathrm{1}\right)!}{{m}!\left({n}−{m}\right)!} \\ $$$$=\frac{\mathrm{2}\left({m}+\mathrm{1}\right)}{\left({n}−{m}\right)}=\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\frac{{m}+\mathrm{1}}{{n}−{m}}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{5}{n}−\mathrm{13}{m}=\mathrm{8} \\ $$$$ \\ $$$$\Rightarrow{n}=\mathrm{13}{k}−\mathrm{1}\:{with}\:{k}\geqslant\mathrm{1} \\ $$$$\Rightarrow{m}=\mathrm{5}{k}−\mathrm{1} \\ $$$$ \\ $$$${n}_{{min}} =\mathrm{13}−\mathrm{1}=\mathrm{12} \\ $$$${m}_{{min}} =\mathrm{5}−\mathrm{1}=\mathrm{4} \\ $$
Commented by ZiYangLee last updated on 15/Sep/21
wow nice... !
$${wow}\:{nice}…\:! \\ $$
Commented by Tawa11 last updated on 15/Sep/21
Weldone sir
$$\mathrm{Weldone}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *