Question Number 175045 by 2kdw last updated on 17/Aug/22
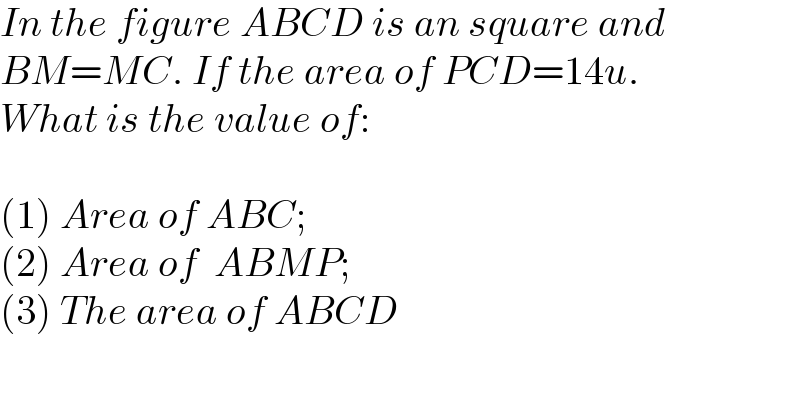
$${In}\:{the}\:{figure}\:{ABCD}\:{is}\:{an}\:{square}\:{and} \\ $$$${BM}={MC}.\:{If}\:{the}\:{area}\:{of}\:{PCD}=\mathrm{14}{u}.\: \\ $$$${What}\:{is}\:{the}\:{value}\:{of}: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{Area}\:{of}\:{ABC}; \\ $$$$\left(\mathrm{2}\right)\:{Area}\:{of}\:\:{ABMP}; \\ $$$$\left(\mathrm{3}\right)\:{The}\:{area}\:{of}\:{ABCD} \\ $$$$ \\ $$
Commented by 2kdw last updated on 17/Aug/22

Commented by mr W last updated on 17/Aug/22
Commented by mr W last updated on 17/Aug/22
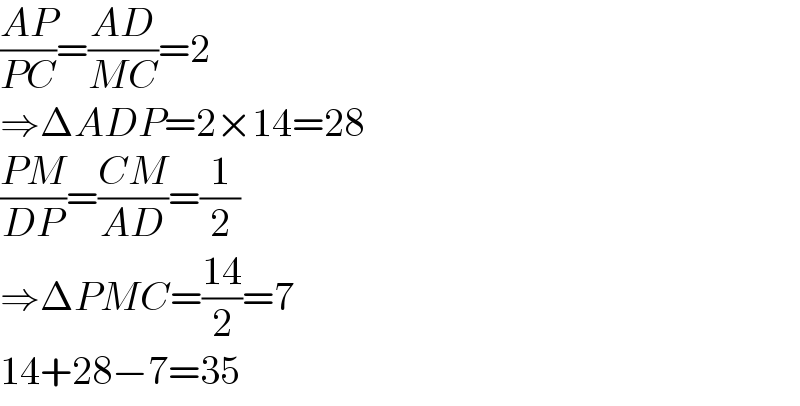
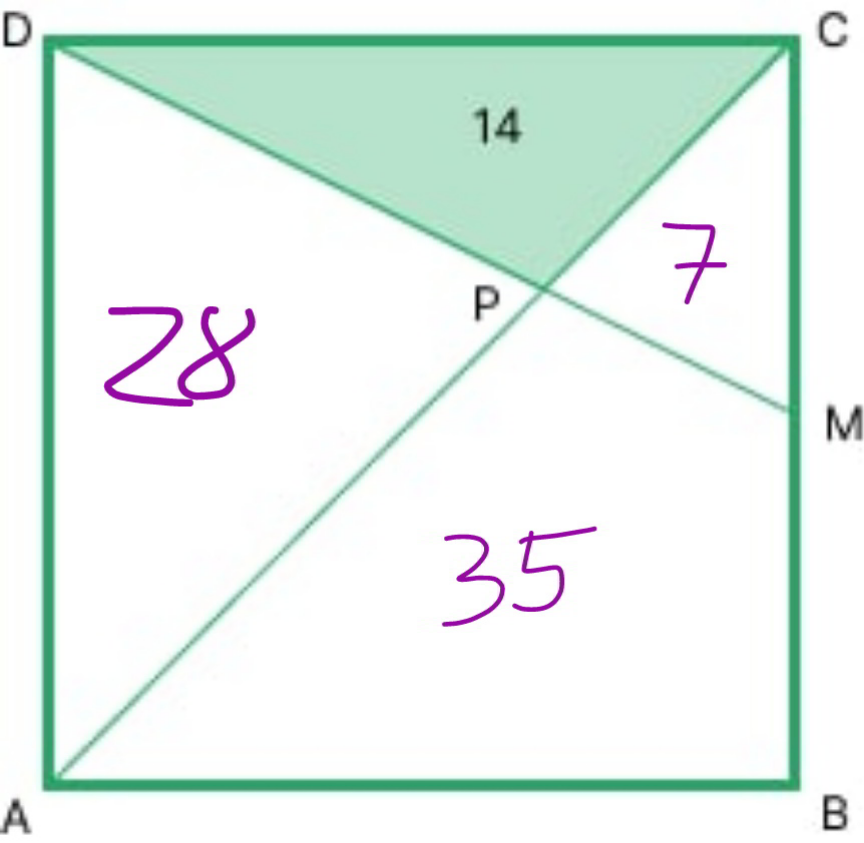
$$\frac{{AP}}{{PC}}=\frac{{AD}}{{MC}}=\mathrm{2} \\ $$$$\Rightarrow\Delta{ADP}=\mathrm{2}×\mathrm{14}=\mathrm{28} \\ $$$$\frac{{PM}}{{DP}}=\frac{{CM}}{{AD}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\Delta{PMC}=\frac{\mathrm{14}}{\mathrm{2}}=\mathrm{7} \\ $$$$\mathrm{14}+\mathrm{28}−\mathrm{7}=\mathrm{35} \\ $$
Commented by 2kdw last updated on 17/Aug/22

$$ \\ $$$${Thank}\:{you},\:{Sir}. \\ $$$$ \\ $$
Commented by Tawa11 last updated on 17/Aug/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
