Menu Close

In-the-following-figure-if-S-1-S-2-S-3-6-pi-find-the-area-of-the-circular-crown-

Tinku Tara 0 Comments
Pin




Question Number 176741 by HeferH last updated on 26/Sep/22
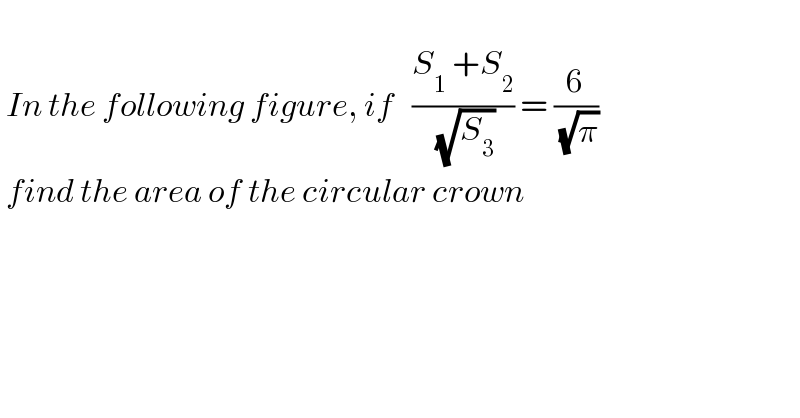
In the following figure, if ((S_1 +S_2 )/( (√S_3 ))) = (6/( (√π))) find the area of the circular crown
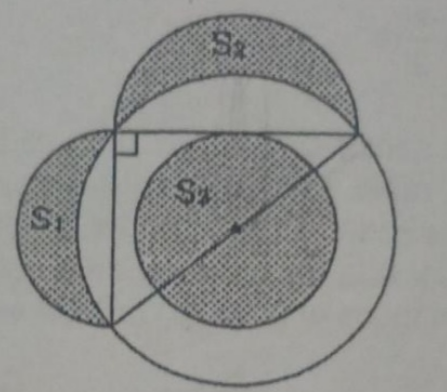
$$\: \\ $$$$\:{In}\:{the}\:{following}\:{figure},\:{if}\:\:\:\frac{{S}_{\mathrm{1}} \:+{S}_{\mathrm{2}} }{\:\sqrt{{S}_{\mathrm{3}} }}\:=\:\frac{\mathrm{6}}{\:\sqrt{\pi}} \\ $$$$\:{find}\:{the}\:{area}\:{of}\:{the}\:{circular}\:{crown}\: \\ $$$$\: \\ $$
Commented by HeferH last updated on 26/Sep/22
Answered by HeferH last updated on 26/Sep/22
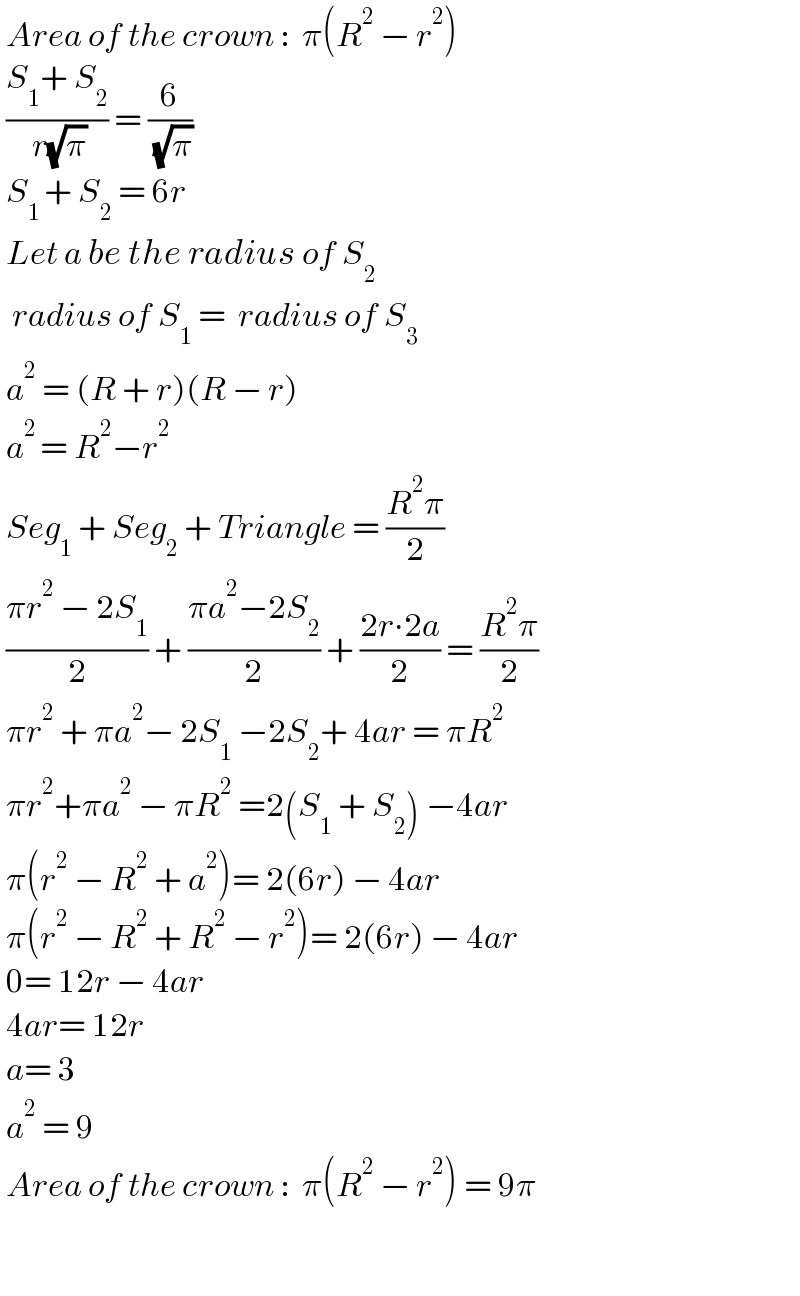
Area of the crown : π(R^2 − r^2 ) ((S_1 + S_2 )/( r(√π))) = (6/( (√π))) S_(1 ) + S_2 = 6r Let a be the radius of S_2 radius of S_1 = radius of S_3 a^2 = (R + r)(R − r) a^(2 ) = R^2 −r^2 Seg_1 + Seg_2 + Triangle = ((R^2 π)/2) ((πr^2 − 2S_1 )/2) + ((πa^2 −2S_2 )/2) + ((2r∙2a)/2) = ((R^2 π)/2) πr^2 + πa^2 − 2S_1 −2S_2 + 4ar = πR^2 πr^2 +πa^2 − πR^2 =2(S_1 + S_2 ) −4ar π(r^2 − R^2 + a^2 )= 2(6r) − 4ar π(r^2 − R^2 + R^2 − r^2 )= 2(6r) − 4ar 0= 12r − 4ar 4ar= 12r a= 3 a^2 = 9 Area of the crown : π(R^2 − r^2 ) = 9π
$$\:{Area}\:{of}\:{the}\:{crown}\::\:\:\pi\left({R}^{\mathrm{2}} \:−\:{r}^{\mathrm{2}} \right) \\ $$$$\:\frac{{S}_{\mathrm{1}} +\:{S}_{\mathrm{2}} }{\:{r}\sqrt{\pi}}\:=\:\frac{\mathrm{6}}{\:\sqrt{\pi}} \\ $$$$\:{S}_{\mathrm{1}\:} +\:{S}_{\mathrm{2}} \:=\:\mathrm{6}{r} \\ $$$$\:{Let}\:{a}\:{be}\:{the}\:{radius}\:{of}\:{S}_{\mathrm{2}} \: \\ $$$$\:\:{radius}\:{of}\:{S}_{\mathrm{1}} \:=\:\:{radius}\:{of}\:{S}_{\mathrm{3}} \\ $$$$\:{a}^{\mathrm{2}} \:=\:\left({R}\:+\:{r}\right)\left({R}\:−\:{r}\right) \\ $$$$\:{a}^{\mathrm{2}\:} =\:{R}^{\mathrm{2}} −{r}^{\mathrm{2}} \\ $$$$\:{Seg}_{\mathrm{1}} \:+\:{Seg}_{\mathrm{2}} \:+\:{Triangle}\:=\:\frac{{R}^{\mathrm{2}} \pi}{\mathrm{2}} \\ $$$$\:\frac{\pi{r}^{\mathrm{2}} \:−\:\mathrm{2}{S}_{\mathrm{1}} }{\mathrm{2}}\:+\:\frac{\pi{a}^{\mathrm{2}} −\mathrm{2}{S}_{\mathrm{2}} }{\mathrm{2}}\:+\:\frac{\mathrm{2}{r}\centerdot\mathrm{2}{a}}{\mathrm{2}}\:=\:\frac{{R}^{\mathrm{2}} \pi}{\mathrm{2}} \\ $$$$\:\pi{r}^{\mathrm{2}} \:+\:\pi{a}^{\mathrm{2}} −\:\mathrm{2}{S}_{\mathrm{1}} \:−\mathrm{2}{S}_{\mathrm{2}} +\:\mathrm{4}{ar}\:=\:\pi{R}^{\mathrm{2}} \\ $$$$\:\pi{r}^{\mathrm{2}} +\pi{a}^{\mathrm{2}} \:−\:\pi{R}^{\mathrm{2}} \:=\mathrm{2}\left({S}_{\mathrm{1}} \:+\:{S}_{\mathrm{2}} \right)\:−\mathrm{4}{ar} \\ $$$$\:\pi\left({r}^{\mathrm{2}} \:−\:{R}^{\mathrm{2}} \:+\:{a}^{\mathrm{2}} \right)=\:\mathrm{2}\left(\mathrm{6}{r}\right)\:−\:\mathrm{4}{ar} \\ $$$$\:\pi\left({r}^{\mathrm{2}} \:−\:{R}^{\mathrm{2}} \:+\:{R}^{\mathrm{2}} \:−\:{r}^{\mathrm{2}} \right)=\:\mathrm{2}\left(\mathrm{6}{r}\right)\:−\:\mathrm{4}{ar} \\ $$$$\:\mathrm{0}=\:\mathrm{12}{r}\:−\:\mathrm{4}{ar} \\ $$$$\:\mathrm{4}{ar}=\:\mathrm{12}{r} \\ $$$$\:{a}=\:\mathrm{3} \\ $$$$\:{a}^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$$\:{Area}\:{of}\:{the}\:{crown}\::\:\:\pi\left({R}^{\mathrm{2}} \:−\:{r}^{\mathrm{2}} \right)\:=\:\mathrm{9}\pi \\ $$$$\: \\ $$$$\: \\ $$
Commented by Tawa11 last updated on 03/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *