Question Number 164590 by Zaynal last updated on 19/Jan/22
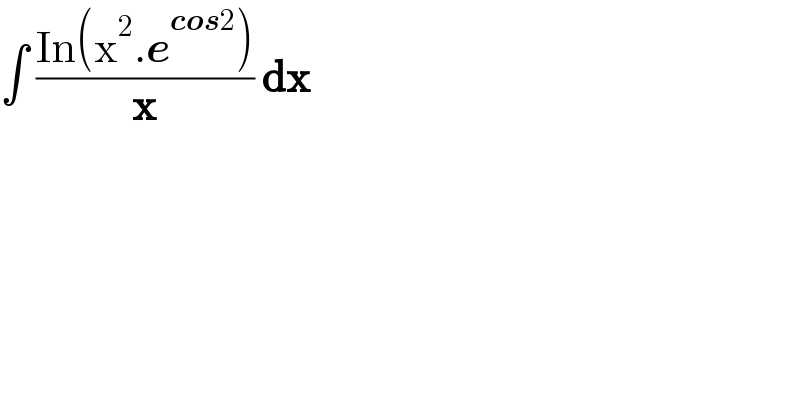
$$\int\:\frac{\mathrm{In}\left(\mathrm{x}^{\mathrm{2}} .\boldsymbol{{e}}^{\boldsymbol{{cos}}\mathrm{2}} \right)}{\boldsymbol{\mathrm{x}}}\:\boldsymbol{\mathrm{dx}} \\ $$
Answered by mahdipoor last updated on 19/Jan/22
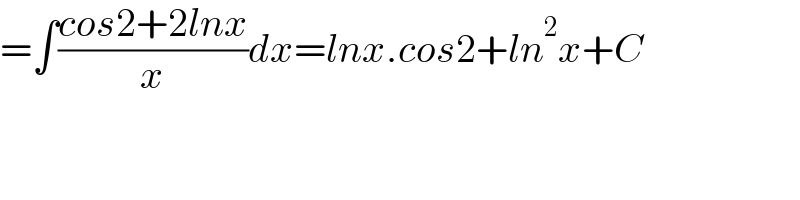
$$=\int\frac{{cos}\mathrm{2}+\mathrm{2}{lnx}}{{x}}{dx}={lnx}.{cos}\mathrm{2}+{ln}^{\mathrm{2}} {x}+{C} \\ $$
