ind-the-value-of-f-a-0-dx-x-2-a-2-x-2-dx-witha-gt-0-2-calculate-f-a-

Question Number 37902 by math khazana by abdo last updated on 19/Jun/18

i n d t h e v a l u e o f f (a) = \int_{0}^{+ \infty} \frac{d x}{x^{2} + \sqrt{a^{2} + x^{2}}} d x

w i t h a > 0

2) c a l c u l a t e f^{^{'}} (a) .

Commented by prof Abdo imad last updated on 19/Jun/18

c h a n g e m e n t x = a t a n t g i v e

f (a) = \int_{0}^{\frac{π}{2}} \frac{1}{a^{2} {t a n}^{2} t + a c o s t} a (1 + {t a n}^{2} t) d t

= \int_{0}^{\frac{π}{2}} \frac{1 + {t a n}^{2} t}{a t a n t + c o s t} d t c h a n g . t a n (\frac{t}{2}) = u

g i v e

f (a) = \int_{0}^{1} \frac{1 + {(\frac{2 u}{1 - u^{2}})}^{2}}{a \frac{2 u}{1 - u^{2}} + \frac{1 - u^{2}}{1 + u^{2}}} \frac{2 d u}{1 + u^{2}}

= 2 \int_{0}^{1} \frac{{(1 - u^{2})}^{2} + 4 u^{2}}{(1 + u^{2}) {(1 - u^{2})}^{2} {\frac{2 a u}{1 - u^{2}} + \frac{1 - u^{2}}{1 + u^{2}}}} d u

= 2 \int_{0}^{1} \frac{{(1 - u^{2})}^{2} + 4 u^{2}}{2 a u (1 - u^{4}) + {(1 - u^{2})}^{3}} d u

= 2 \int_{0}^{1} \frac{{(1 + u^{2})}^{2}}{2 a u - 2 {a u}^{5} - (u^{6} + 3 u^{4} - 3 u^{2} - 1)} d u

= 2 \int_{0}^{1} \frac{u^{4} + 2 u^{2} + 1}{- u^{6} - 2 {a u}^{5} + 3 u^{2} + 2 a u + 1} d u

= - 2 \int_{0}^{1} \frac{u^{4} + 2 u^{2} + 1}{u^{6} + 2 {a u}^{5} - 3 u^{2} - 2 a u - 1} d u \dots b e

c o n t i n u e d \dots

Answered by ajfour last updated on 19/Jun/18

l e t x = a \tan θ

f (a) = \int_{0}^{π / 2} \frac{\sec^{2} θ d θ}{a \tan^{2} θ + \sec θ}

= \int_{0}^{π / 2} \frac{d θ}{a \sin^{2} θ + \cos θ}

l e t \tan \frac{θ}{2} = t

= \int_{0}^{1} \frac{\frac{2 d t}{1 + t^{2}}}{a {(\frac{2 t}{1 + t^{2}})}^{2} + \frac{1 - t^{2}}{1 + t^{2}}}

= \int_{0}^{1} \frac{2 (1 + t^{2}) d t}{4 {a t}^{2} + 1 - t^{4}}

l e t t^{4} - 4 {a t}^{2} + 1 = 0

\Rightarrow t^{2} = \frac{4 a \pm \sqrt{16 a^{2} - 4}}{2}

s a y α, β = 2 a \pm \sqrt{4 a^{2} - 1}

f (a) = - \int_{0}^{1} \frac{1 + t^{2}}{(t^{2} - α) (t^{2} - β)} d t

= - \frac{α + 1}{α - β} \int_{0}^{1} \frac{d t}{t^{2} - α} + \frac{1 + β}{α - β} \int_{0}^{1} \frac{d t}{t^{2} - β}

= - \frac{α + 1}{α - β} \times \frac{1}{2 \sqrt{α}} \ln ∣ \frac{t - \sqrt{α}}{t + \sqrt{α}} ∣_{0}^{1}

+ \frac{1 + β}{α - β} \times \frac{1}{2 \sqrt{β}} \ln ∣ \frac{t - \sqrt{β}}{t + \sqrt{β}} ∣_{0}^{1}

n o t s a t i s f a c t o r y, i g u e s s!

Commented by tanmay.chaudhury50@gmail.com last updated on 19/Jun/18

\int_{0}^{1} \frac{2 (\frac{1}{t^{2}} + 1) d t}{4 a + \frac{1}{t^{2}} - t^{2}}

\int_{0}^{1} \frac{2 d (t - \frac{1}{t})}{4 a - (t - \frac{1}{t}) (t + \frac{1}{t})}

2 \int_{0}^{1} \frac{d (t - \frac{1}{t})}{4 a - (t - \frac{1}{t}) \sqrt{{(t - \frac{1}{t})}^{2} + 4}}

2 \int_{- \infty}^{0} \frac{d k}{4 a - k \sqrt{k^{2} + 4}}

c o n t d

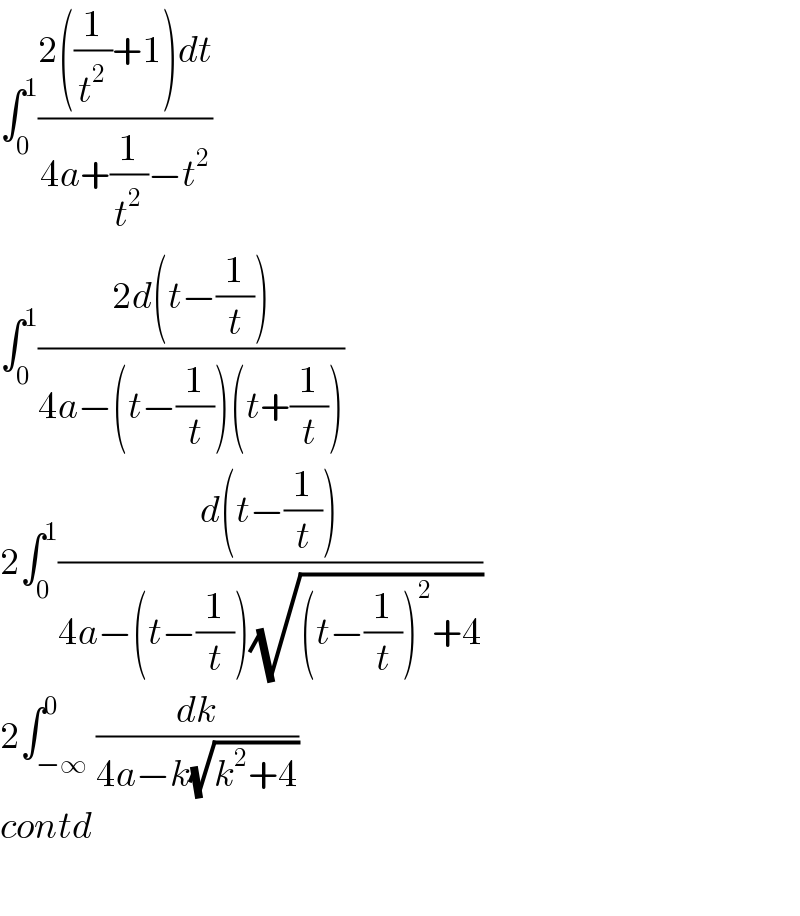
Answered by MJS last updated on 19/Jun/18

this is the method :

\int \frac{d x}{x^{2} + \sqrt{x^{2} + a^{2}}} = \int \frac{x^{2}}{x^{4} - x^{2} - a^{2}} d x - \int \frac{\sqrt{x^{2} + a^{2}}}{x^{4} - x^{2} - a^{2}} d x

\int \frac{x^{2}}{x^{4} - x^{2} - a^{2}} d x =

= \underset{i = 1}{\sum^{4}} \int \frac{N_{i}}{x - r_{i}} d x = \underset{i = 1}{\sum^{4}} N_{i} \ln ∣ x - r_{i} ∣

\int \frac{\sqrt{x^{2} + a^{2}}}{x^{4} - x^{2} - a^{2}} d x =

[t = \frac{x}{\sqrt{x^{2} + a^{2}}} \to d x = \frac{d t}{a^{2}} \sqrt{{(x^{2} + a^{2})}^{3}}]

= \frac{1}{a^{2}} \int \frac{d t}{t^{4} + \frac{1}{a^{2}} t^{2} - \frac{1}{a^{2}}} =

= \frac{N_{5}}{a^{2}} (\int \frac{d t}{t - r_{5}} - \int \frac{d t}{t + r_{5}}) + \frac{N_{6}}{a^{2}} \int \frac{d t}{t^{2} + r_{6}} =

[r_{6} > 0]

= \frac{N_{5}}{a^{2}} \ln ∣ \frac{t - r_{5}}{t + r_{5}} ∣ + \frac{N_{6}}{a^{2} \sqrt{r_{6}}} \arctan \frac{t}{\sqrt{r_{6}}} =

= \frac{N_{5}}{a^{2}} \ln ∣ \frac{\frac{x}{\sqrt{x^{2} + a^{2}}} - r_{5}}{\frac{x}{\sqrt{x^{2} + a^{2}}} + r_{5}} ∣ + \frac{N_{6}}{a^{2} \sqrt{r_{6}}} \arctan \frac{x}{\sqrt{r_{6} (x^{2} + a^{2})}}

Commented by MJS last updated on 20/Jun/18

r_{1} = - \frac{\sqrt{2}}{2} \sqrt{1 - \sqrt{4 a^{2} + 1}}

r_{2} = - \frac{\sqrt{2}}{2} \sqrt{1 + \sqrt{4 a^{2} + 1}}

r_{3} = \frac{\sqrt{2}}{2} \sqrt{1 - \sqrt{4 a^{2} + 1}}

r_{4} = \frac{\sqrt{2}}{2} \sqrt{1 + \sqrt{4 a^{2} + 1}}

r_{5} = \frac{\sqrt{2}}{2 a} \sqrt{- 1 + \sqrt{4 a^{2} + 1}}

r_{6} = \frac{1 + \sqrt{4 a^{2} + 1}}{2 a^{2}}

N_{1} = \frac{\sqrt{2 - 2 \sqrt{4 a^{2} + 1}}}{4 \sqrt{4 a^{2} + 1}}

N_{2} = - \frac{\sqrt{2 + 2 \sqrt{4 a^{2} + 1}}}{4 \sqrt{4 a^{2} + 1}}

N_{3} = - \frac{\sqrt{2 - 2 \sqrt{4 a^{2} + 1}}}{4 \sqrt{4 a^{2} + 1}}

N_{4} = \frac{\sqrt{2 + 2 \sqrt{4 a^{2} + 1}}}{4 \sqrt{4 a^{2} + 1}}

N_{5} = \frac{a^{3} \sqrt{2}}{2 \sqrt{(4 a^{2} + 1) (- 1 + \sqrt{4 a^{2} + 1})}}

N_{6} = - \frac{a^{2}}{\sqrt{4 a^{2} + 1}}

Commented by math khazana by abdo last updated on 20/Jun/18

t h a n k y o u s i r M j s