Question Number 104190 by mr W last updated on 19/Jul/20
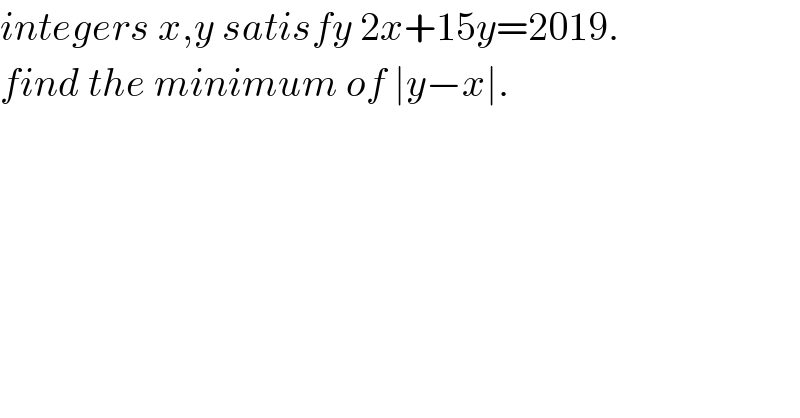
$${integers}\:{x},{y}\:{satisfy}\:\mathrm{2}{x}+\mathrm{15}{y}=\mathrm{2019}. \\ $$$${find}\:{the}\:{minimum}\:{of}\:\mid{y}−{x}\mid. \\ $$
Commented by mr W last updated on 20/Jul/20

$${thank}\:{you}\:{all}! \\ $$$$\mathrm{2}\:{is}\:{correct}. \\ $$
Answered by mathmax by abdo last updated on 19/Jul/20
![let consider congruence modulo 2(prime) e ⇒0 +15^− y^− =2019^− ⇒y^− =1^− ⇒y =2k+1 (k ∈Z) 2x+15y =2019 ⇒2x +15(2k+1) =2019 ⇒2x +30k +15 =2019 ⇒ 2x =2019−15 −30k =2004−30k ⇒x =1002−15k ⇒ min∣y−x∣ =min∣2k+1−1002+15k∣ =min∣17k−1001∣=0 if k=[((1001)/(17))]](https://www.tinkutara.com/question/Q104194.png)
$$\mathrm{let}\:\mathrm{consider}\:\mathrm{congruence}\:\mathrm{modulo}\:\mathrm{2}\left(\mathrm{prime}\right) \\ $$$$\mathrm{e}\:\Rightarrow\mathrm{0}\:+\mathrm{1}\overset{−} {\mathrm{5}}\:\overset{−} {\mathrm{y}}\:=\mathrm{201}\overset{−} {\mathrm{9}}\:\Rightarrow\overset{−} {\mathrm{y}}\:=\overset{−} {\mathrm{1}}\:\Rightarrow\mathrm{y}\:=\mathrm{2k}+\mathrm{1}\:\:\:\left(\mathrm{k}\:\in\mathrm{Z}\right) \\ $$$$\mathrm{2x}+\mathrm{15y}\:=\mathrm{2019}\:\Rightarrow\mathrm{2x}\:+\mathrm{15}\left(\mathrm{2k}+\mathrm{1}\right)\:=\mathrm{2019}\:\Rightarrow\mathrm{2x}\:+\mathrm{30k}\:+\mathrm{15}\:=\mathrm{2019}\:\Rightarrow \\ $$$$\mathrm{2x}\:=\mathrm{2019}−\mathrm{15}\:−\mathrm{30k}\:=\mathrm{2004}−\mathrm{30k}\:\Rightarrow\mathrm{x}\:=\mathrm{1002}−\mathrm{15k}\:\Rightarrow \\ $$$$\mathrm{min}\mid\mathrm{y}−\mathrm{x}\mid\:=\mathrm{min}\mid\mathrm{2k}+\mathrm{1}−\mathrm{1002}+\mathrm{15k}\mid\:=\mathrm{min}\mid\mathrm{17k}−\mathrm{1001}\mid=\mathrm{0}\:\mathrm{if}\:\mathrm{k}=\left[\frac{\mathrm{1001}}{\mathrm{17}}\right] \\ $$
Answered by floor(10²Eta[1]) last updated on 20/Jul/20

$$\mathrm{gcd}\left(\mathrm{2},\:\mathrm{15}\right)=\mathrm{1}\mid\mathrm{2019}\Rightarrow\mathrm{has}\:\mathrm{solution}. \\ $$$$\mathrm{15}=\mathrm{2}.\mathrm{7}+\mathrm{1}\Rightarrow\mathrm{15}−\mathrm{2}.\mathrm{7}=\mathrm{1}\:\left(×\mathrm{2019}\right) \\ $$$$\Rightarrow\mathrm{2}.\left(−\mathrm{14133}\right)+\mathrm{15}.\left(\mathrm{2019}\right)=\mathrm{2019} \\ $$$$\left(\mathrm{x}_{\mathrm{0}} ,\:\mathrm{y}_{\mathrm{0}} \right)=\left(−\mathrm{14133},\:\mathrm{2019}\right)\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}. \\ $$$$\mathrm{the}\:\mathrm{general}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{a}\:\mathrm{diophantine} \\ $$$$\mathrm{equation}\:\mathrm{of}\:\mathrm{the}\:\mathrm{form}\:\mathrm{ax}+\mathrm{by}=\mathrm{c}\:\mathrm{is}: \\ $$$$\left(\mathrm{x},\:\mathrm{y}\right)=\left(\mathrm{x}_{\mathrm{0}} −\frac{\mathrm{bk}}{\mathrm{gcd}\left(\mathrm{a},\:\mathrm{b}\right)},\:\mathrm{y}_{\mathrm{0}} +\frac{\mathrm{ak}}{\mathrm{gcd}\left(\mathrm{a},\:\mathrm{b}\right)}\right),\:\mathrm{k}\in\mathbb{Z} \\ $$$$\Rightarrow\left(\mathrm{x},\:\mathrm{y}\right)=\left(−\mathrm{14133}−\mathrm{15k},\:\mathrm{2019}+\mathrm{2k}\right) \\ $$$$\mathrm{min}\mid\mathrm{y}−\mathrm{x}\mid=\mathrm{min}\mid\mathrm{2019}+\mathrm{2k}−\left(−\mathrm{14133}−\mathrm{15k}\right)\mid \\ $$$$=\mathrm{min}\mid\mathrm{16152}+\mathrm{17k}\mid \\ $$$$\mathrm{16152}+\mathrm{17k}>\mathrm{0}\Rightarrow\mathrm{k}\geqslant−\mathrm{950} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{is}\:\mathrm{when}\:\mathrm{k}=−\mathrm{950} \\ $$$$\Rightarrow\mathrm{16152}+\mathrm{17}\left(−\mathrm{950}\right)=\mathrm{2} \\ $$
Answered by 1549442205PVT last updated on 20/Jul/20
![We have x=((2019−15y)/2)=1009−7y+((1−y)/2)∈Z ⇒put ((1−y)/2)=a(a∈Z)⇒y=1−2a ⇒x=1009−7(1−2a)+a=15a+1002 ⇒∣y−x∣=∣17a+1001∣=∣17(a+59)−2∣ Put ∣17(a+59)−2∣=m⇒m^2 =17^2 (a+59)^2 −68(a+59)+4 =17(a+59)[17(a+59)−4]+4≥4⇒m≥2 Since ,a+59∈Z,if a+59>0 then a+59≥1 ⇒17(a+59)−4≥13⇒17(a+59)[17(a+59)−4≥17×13 if a+59<0 then (a+59)≤−1⇒17(a+59)−4≤−21 ⇒17(a+59)[17(a+59)−4≥(−17)×(−21) and when a−59=0 we get m^2 =4 Therefore,m≥2 which means ∣y−x∣_(min) =2 when a=−59⇔ { ((x=117)),((y=119)) :} other way: x=((2019−15y)/2)⇒∣y−x∣=∣((17y−2019)/2)∣ =∣8y−1009+((y−1)/2)∣.Put ((y−1)/2)=k We get y=2k+1⇒∣y−x∣=∣8(2k+1)−1009+k∣ =∣17k−1001∣=∣17(k−59)+2∣ i)If k=59 then ∣17(k−59)+2∣=2 ii)If k≥60 then ∣17(k−59)+2∣≥19 iii)If k≤58 then 17(k−59)+2≤−17+2=−15 ⇒∣17(k−59)+2∣≥15 Compare three above cases we infer ∣17(k−59)+2∣_(min) =2 when k=59⇒y=2k+1=119 x=((2019−15y)/2)=117.Thus,∣y−x∣_(min) =2 when⇔(x;y)=(117,119)](https://www.tinkutara.com/question/Q104214.png)
$$\mathrm{We}\:\mathrm{have}\:\mathrm{x}=\frac{\mathrm{2019}−\mathrm{15y}}{\mathrm{2}}=\mathrm{1009}−\mathrm{7y}+\frac{\mathrm{1}−\mathrm{y}}{\mathrm{2}}\in\mathbb{Z} \\ $$$$\Rightarrow\mathrm{put}\:\frac{\mathrm{1}−\mathrm{y}}{\mathrm{2}}=\mathrm{a}\left(\mathrm{a}\in\mathbb{Z}\right)\Rightarrow\mathrm{y}=\mathrm{1}−\mathrm{2a} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{1009}−\mathrm{7}\left(\mathrm{1}−\mathrm{2a}\right)+\mathrm{a}=\mathrm{15a}+\mathrm{1002} \\ $$$$\Rightarrow\mid\mathrm{y}−\mathrm{x}\mid=\mid\mathrm{17a}+\mathrm{1001}\mid=\mid\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{2}\mid \\ $$$$\mathrm{Put}\:\mid\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{2}\mid=\mathrm{m}\Rightarrow\mathrm{m}^{\mathrm{2}} =\mathrm{17}^{\mathrm{2}} \left(\mathrm{a}+\mathrm{59}\right)^{\mathrm{2}} −\mathrm{68}\left(\mathrm{a}+\mathrm{59}\right)+\mathrm{4} \\ $$$$=\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)\left[\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{4}\right]+\mathrm{4}\geqslant\mathrm{4}\Rightarrow\mathrm{m}\geqslant\mathrm{2} \\ $$$$\mathrm{Since}\:,\mathrm{a}+\mathrm{59}\in\mathbb{Z},\mathrm{if}\:\mathrm{a}+\mathrm{59}>\mathrm{0}\:\mathrm{then}\:\mathrm{a}+\mathrm{59}\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{4}\geqslant\mathrm{13}\Rightarrow\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)\left[\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{4}\geqslant\mathrm{17}×\mathrm{13}\right. \\ $$$$\mathrm{if}\:\mathrm{a}+\mathrm{59}<\mathrm{0}\:\mathrm{then}\:\left(\mathrm{a}+\mathrm{59}\right)\leqslant−\mathrm{1}\Rightarrow\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{4}\leqslant−\mathrm{21} \\ $$$$\Rightarrow\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)\left[\mathrm{17}\left(\mathrm{a}+\mathrm{59}\right)−\mathrm{4}\geqslant\left(−\mathrm{17}\right)×\left(−\mathrm{21}\right)\right. \\ $$$$\mathrm{and}\:\mathrm{when}\:\mathrm{a}−\mathrm{59}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{m}^{\mathrm{2}} =\mathrm{4} \\ $$$$\mathrm{Therefore},\mathrm{m}\geqslant\mathrm{2}\:\mathrm{which}\:\mathrm{means}\:\mid\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{x}}\mid_{\boldsymbol{\mathrm{min}}} =\mathrm{2} \\ $$$$\mathrm{when}\:\mathrm{a}=−\mathrm{59}\Leftrightarrow\begin{cases}{\mathrm{x}=\mathrm{117}}\\{\mathrm{y}=\mathrm{119}}\end{cases} \\ $$$$\boldsymbol{\mathrm{other}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\mathrm{x}=\frac{\mathrm{2019}−\mathrm{15y}}{\mathrm{2}}\Rightarrow\mid\mathrm{y}−\mathrm{x}\mid=\mid\frac{\mathrm{17y}−\mathrm{2019}}{\mathrm{2}}\mid \\ $$$$=\mid\mathrm{8y}−\mathrm{1009}+\frac{\mathrm{y}−\mathrm{1}}{\mathrm{2}}\mid.\mathrm{Put}\:\frac{\mathrm{y}−\mathrm{1}}{\mathrm{2}}=\mathrm{k} \\ $$$$\mathrm{We}\:\mathrm{get} \\ $$$$\mathrm{y}=\mathrm{2k}+\mathrm{1}\Rightarrow\mid\mathrm{y}−\mathrm{x}\mid=\mid\mathrm{8}\left(\mathrm{2k}+\mathrm{1}\right)−\mathrm{1009}+\mathrm{k}\mid \\ $$$$=\mid\mathrm{17k}−\mathrm{1001}\mid=\mid\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\mid \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{k}=\mathrm{59}\:\mathrm{then}\:\mid\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\mid=\mathrm{2} \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{k}\geqslant\mathrm{60}\:\mathrm{then}\:\mid\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\mid\geqslant\mathrm{19} \\ $$$$\left.\mathrm{iii}\right)\mathrm{If}\:\mathrm{k}\leqslant\mathrm{58}\:\mathrm{then}\:\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\leqslant−\mathrm{17}+\mathrm{2}=−\mathrm{15} \\ $$$$\Rightarrow\mid\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\mid\geqslant\mathrm{15} \\ $$$$\mathrm{Compare}\:\mathrm{three}\:\mathrm{above}\:\mathrm{cases}\:\mathrm{we}\:\mathrm{infer} \\ $$$$\mid\mathrm{17}\left(\mathrm{k}−\mathrm{59}\right)+\mathrm{2}\mid_{\boldsymbol{\mathrm{min}}} =\mathrm{2}\:\mathrm{when}\:\mathrm{k}=\mathrm{59}\Rightarrow\mathrm{y}=\mathrm{2k}+\mathrm{1}=\mathrm{119} \\ $$$$\mathrm{x}=\frac{\mathrm{2019}−\mathrm{15y}}{\mathrm{2}}=\mathrm{117}.\boldsymbol{\mathrm{Thus}},\mid\boldsymbol{\mathrm{y}}−\boldsymbol{\mathrm{x}}\mid_{\boldsymbol{\mathrm{min}}} =\mathrm{2} \\ $$$$\boldsymbol{\mathrm{when}}\Leftrightarrow\left(\boldsymbol{\mathrm{x}};\boldsymbol{\mathrm{y}}\right)=\left(\mathrm{117},\mathrm{119}\right) \\ $$$$ \\ $$
