Question Number 55873 by Easyman32 last updated on 05/Mar/19

$${Integrate}..\int\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}\:{dx} \\ $$
Commented by maxmathsup by imad last updated on 05/Mar/19
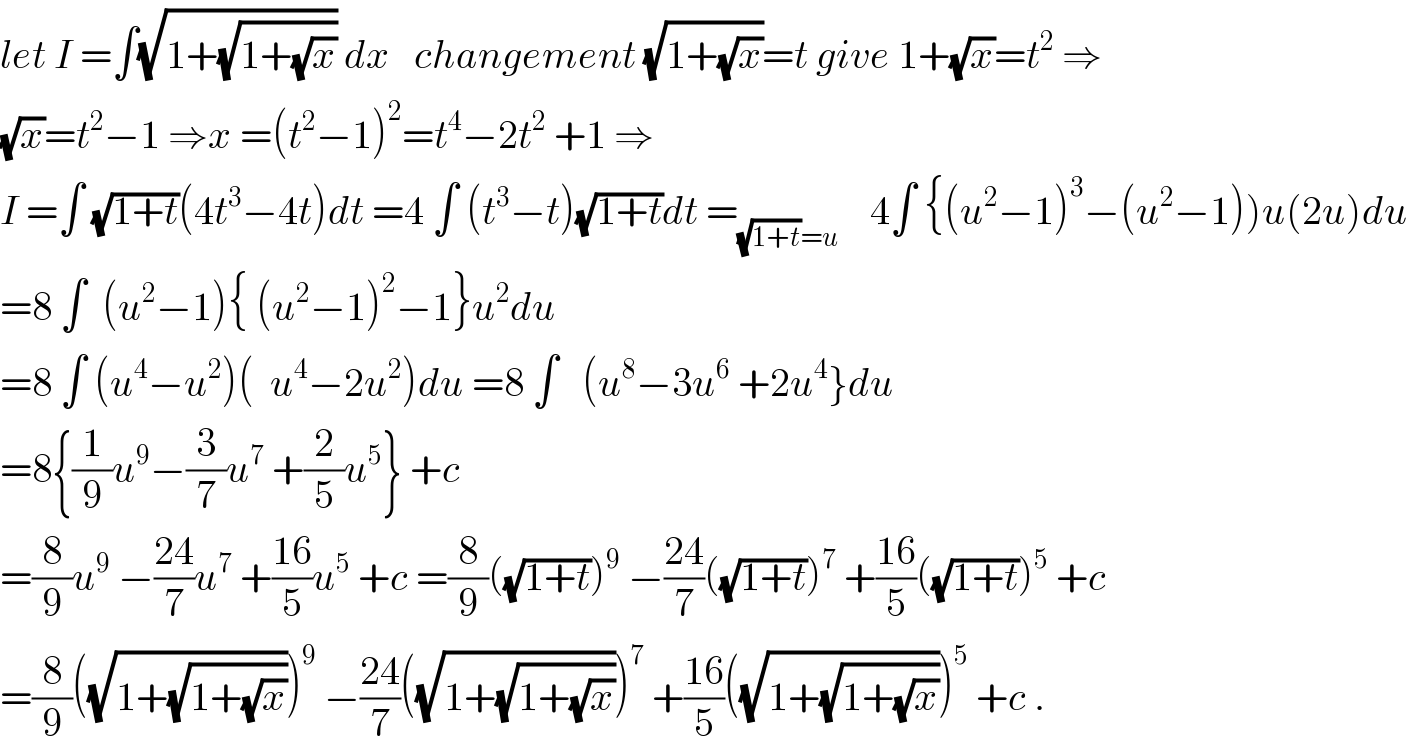
$${let}\:{I}\:=\int\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}\:{dx}\:\:\:{changement}\:\sqrt{\mathrm{1}+\sqrt{{x}}}={t}\:{give}\:\mathrm{1}+\sqrt{{x}}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\sqrt{{x}}={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow{x}\:=\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} ={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}\:\Rightarrow \\ $$$${I}\:=\int\:\sqrt{\mathrm{1}+{t}}\left(\mathrm{4}{t}^{\mathrm{3}} −\mathrm{4}{t}\right){dt}\:=\mathrm{4}\:\int\:\left({t}^{\mathrm{3}} −{t}\right)\sqrt{\mathrm{1}+{t}}{dt}\:=_{\sqrt{\mathrm{1}+{t}}={u}} \:\:\:\:\mathrm{4}\int\:\left\{\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} −\left({u}^{\mathrm{2}} −\mathrm{1}\right)\right){u}\left(\mathrm{2}{u}\right){du} \\ $$$$=\mathrm{8}\:\int\:\:\left({u}^{\mathrm{2}} −\mathrm{1}\right)\left\{\:\left({u}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} −\mathrm{1}\right\}{u}^{\mathrm{2}} {du} \\ $$$$=\mathrm{8}\:\int\:\left({u}^{\mathrm{4}} −{u}^{\mathrm{2}} \right)\left(\:\:{u}^{\mathrm{4}} −\mathrm{2}{u}^{\mathrm{2}} \right){du}\:=\mathrm{8}\:\int\:\:\:\left({u}^{\mathrm{8}} −\mathrm{3}{u}^{\mathrm{6}} \:+\mathrm{2}{u}^{\mathrm{4}} \right\}{du} \\ $$$$=\mathrm{8}\left\{\frac{\mathrm{1}}{\mathrm{9}}{u}^{\mathrm{9}} −\frac{\mathrm{3}}{\mathrm{7}}{u}^{\mathrm{7}} \:+\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}} \right\}\:+{c} \\ $$$$=\frac{\mathrm{8}}{\mathrm{9}}{u}^{\mathrm{9}} \:−\frac{\mathrm{24}}{\mathrm{7}}{u}^{\mathrm{7}} \:+\frac{\mathrm{16}}{\mathrm{5}}{u}^{\mathrm{5}} \:+{c}\:=\frac{\mathrm{8}}{\mathrm{9}}\left(\sqrt{\mathrm{1}+{t}}\right)^{\mathrm{9}} \:−\frac{\mathrm{24}}{\mathrm{7}}\left(\sqrt{\mathrm{1}+{t}}\right)^{\mathrm{7}} \:+\frac{\mathrm{16}}{\mathrm{5}}\left(\sqrt{\mathrm{1}+{t}}\right)^{\mathrm{5}} \:+{c} \\ $$$$=\frac{\mathrm{8}}{\mathrm{9}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}\right)^{\mathrm{9}} \:−\frac{\mathrm{24}}{\mathrm{7}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}\right)^{\mathrm{7}} \:+\frac{\mathrm{16}}{\mathrm{5}}\left(\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}\right)^{\mathrm{5}} \:+{c}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Mar/19
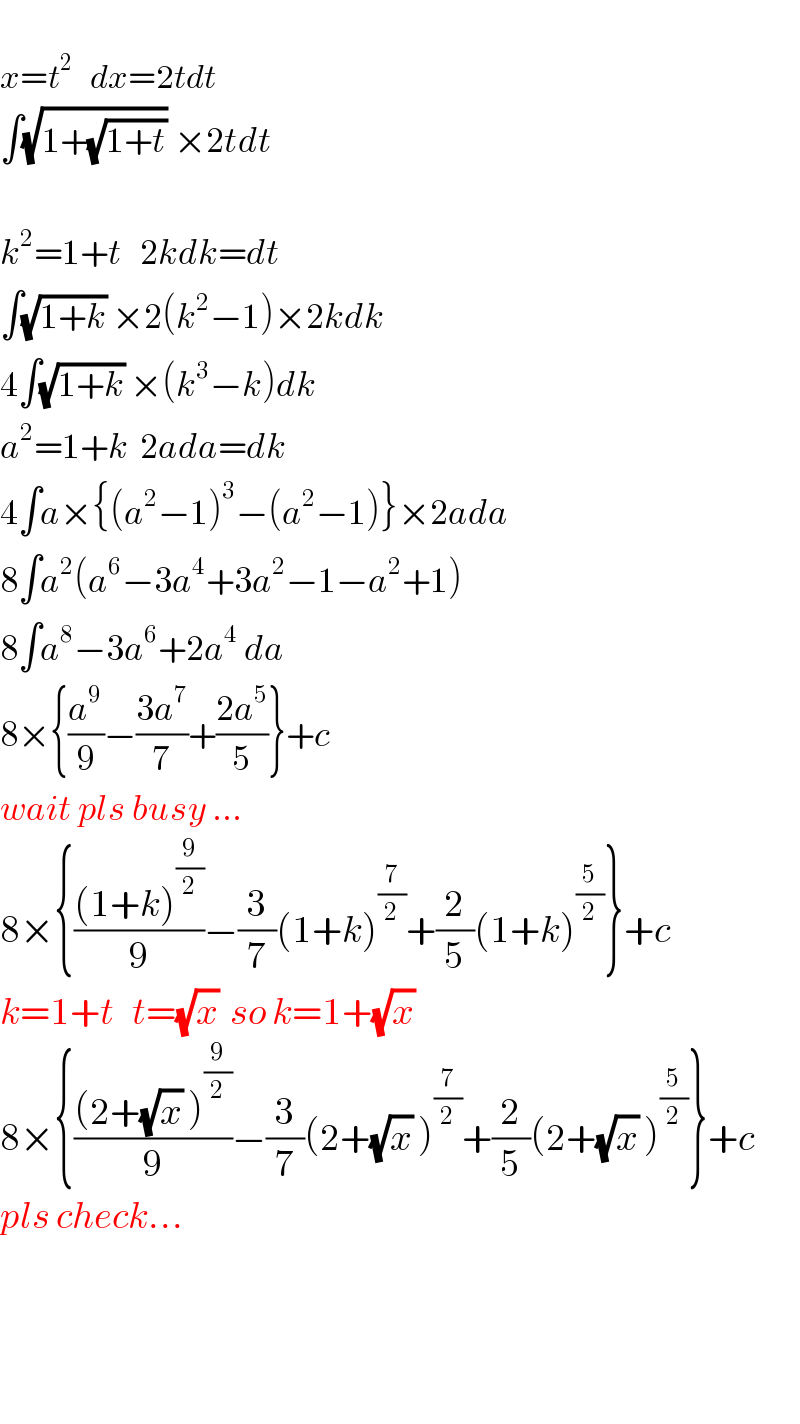
$$ \\ $$$${x}={t}^{\mathrm{2}} \:\:\:{dx}=\mathrm{2}{tdt} \\ $$$$\int\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+{t}}}\:×\mathrm{2}{tdt} \\ $$$$ \\ $$$${k}^{\mathrm{2}} =\mathrm{1}+{t}\:\:\:\mathrm{2}{kdk}={dt} \\ $$$$\int\sqrt{\mathrm{1}+{k}}\:×\mathrm{2}\left({k}^{\mathrm{2}} −\mathrm{1}\right)×\mathrm{2}{kdk} \\ $$$$\mathrm{4}\int\sqrt{\mathrm{1}+{k}}\:×\left({k}^{\mathrm{3}} −{k}\right){dk} \\ $$$${a}^{\mathrm{2}} =\mathrm{1}+{k}\:\:\mathrm{2}{ada}={dk} \\ $$$$\mathrm{4}\int{a}×\left\{\left({a}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} −\left({a}^{\mathrm{2}} −\mathrm{1}\right)\right\}×\mathrm{2}{ada} \\ $$$$\mathrm{8}\int{a}^{\mathrm{2}} \left({a}^{\mathrm{6}} −\mathrm{3}{a}^{\mathrm{4}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{1}−{a}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{8}\int{a}^{\mathrm{8}} −\mathrm{3}{a}^{\mathrm{6}} +\mathrm{2}{a}^{\mathrm{4}} \:{da} \\ $$$$\mathrm{8}×\left\{\frac{{a}^{\mathrm{9}} }{\mathrm{9}}−\frac{\mathrm{3}{a}^{\mathrm{7}} }{\mathrm{7}}+\frac{\mathrm{2}{a}^{\mathrm{5}} }{\mathrm{5}}\right\}+{c} \\ $$$${wait}\:{pls}\:{busy}\:… \\ $$$$\mathrm{8}×\left\{\frac{\left(\mathrm{1}+{k}\right)^{\frac{\mathrm{9}}{\mathrm{2}}} }{\mathrm{9}}−\frac{\mathrm{3}}{\mathrm{7}}\left(\mathrm{1}+{k}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{1}+{k}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \right\}+{c} \\ $$$${k}=\mathrm{1}+{t}\:\:\:{t}=\sqrt{{x}}\:\:{so}\:{k}=\mathrm{1}+\sqrt{{x}}\: \\ $$$$\mathrm{8}×\left\{\frac{\left(\mathrm{2}+\sqrt{{x}}\:\right)^{\frac{\mathrm{9}}{\mathrm{2}}} }{\mathrm{9}}−\frac{\mathrm{3}}{\mathrm{7}}\left(\mathrm{2}+\sqrt{{x}}\:\right)^{\frac{\mathrm{7}}{\mathrm{2}}} +\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{2}+\sqrt{{x}}\:\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \right\}+{c} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 05/Mar/19
![∫(√(1+(√(1+(√x)))))dx= [t=1+(√(1+(√x))) → dx=4(√x)(√(1+(√x)))dt; (√x)=t^2 −2t] =4∫(t−2)(t−1)t^(3/2) dt= =4∫(t^(7/2) −3t^(5/2) +2t^(3/2) )dt= =(8/9)t^(9/2) −((24)/7)t^(7/2) +((16)/5)t^(5/2) = =(8/(315))t^(5/2) (35t^2 −135t+126) please do the inserting...](https://www.tinkutara.com/question/Q55876.png)
$$\int\sqrt{\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{1}+\sqrt{\mathrm{1}+\sqrt{{x}}}\:\rightarrow\:{dx}=\mathrm{4}\sqrt{{x}}\sqrt{\mathrm{1}+\sqrt{{x}}}{dt};\:\sqrt{{x}}={t}^{\mathrm{2}} −\mathrm{2}{t}\right] \\ $$$$=\mathrm{4}\int\left({t}−\mathrm{2}\right)\left({t}−\mathrm{1}\right){t}^{\frac{\mathrm{3}}{\mathrm{2}}} {dt}= \\ $$$$=\mathrm{4}\int\left({t}^{\frac{\mathrm{7}}{\mathrm{2}}} −\mathrm{3}{t}^{\frac{\mathrm{5}}{\mathrm{2}}} +\mathrm{2}{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \right){dt}= \\ $$$$=\frac{\mathrm{8}}{\mathrm{9}}{t}^{\frac{\mathrm{9}}{\mathrm{2}}} −\frac{\mathrm{24}}{\mathrm{7}}{t}^{\frac{\mathrm{7}}{\mathrm{2}}} +\frac{\mathrm{16}}{\mathrm{5}}{t}^{\frac{\mathrm{5}}{\mathrm{2}}} = \\ $$$$=\frac{\mathrm{8}}{\mathrm{315}}{t}^{\frac{\mathrm{5}}{\mathrm{2}}} \left(\mathrm{35}{t}^{\mathrm{2}} −\mathrm{135}{t}+\mathrm{126}\right) \\ $$$$\mathrm{please}\:\mathrm{do}\:\mathrm{the}\:\mathrm{inserting}… \\ $$
