Question Number 154876 by Mr.D.N. last updated on 22/Sep/21
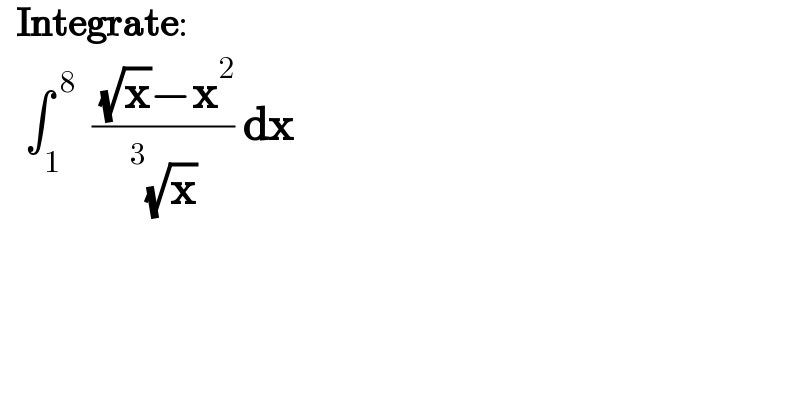
$$\:\:\boldsymbol{\mathrm{Integrate}}: \\ $$$$\:\:\:\int_{\mathrm{1}} ^{\:\mathrm{8}} \:\:\frac{\:\sqrt{\boldsymbol{\mathrm{x}}}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }{\overset{\mathrm{3}} {\:}\sqrt{\boldsymbol{\mathrm{x}}}}\:\boldsymbol{\mathrm{dx}} \\ $$
Answered by MJS_new last updated on 22/Sep/21
![=∫_1 ^8 x^(1/6) −x^(5/3) dx=[(6/7)x^(7/6) −(3/8)x^(8/3) ]_1 ^8 = =((48(√2))/7)−((5403)/(56))](https://www.tinkutara.com/question/Q154891.png)
$$=\underset{\mathrm{1}} {\overset{\mathrm{8}} {\int}}{x}^{\mathrm{1}/\mathrm{6}} −{x}^{\mathrm{5}/\mathrm{3}} {dx}=\left[\frac{\mathrm{6}}{\mathrm{7}}{x}^{\mathrm{7}/\mathrm{6}} −\frac{\mathrm{3}}{\mathrm{8}}{x}^{\mathrm{8}/\mathrm{3}} \right]_{\mathrm{1}} ^{\mathrm{8}} = \\ $$$$=\frac{\mathrm{48}\sqrt{\mathrm{2}}}{\mathrm{7}}−\frac{\mathrm{5403}}{\mathrm{56}} \\ $$
Commented by Mr.D.N. last updated on 23/Sep/21

$$\mathrm{thank}\:\mathrm{you}. \\ $$
