Question Number 22151 by j.masanja06@gmail.com last updated on 12/Oct/17
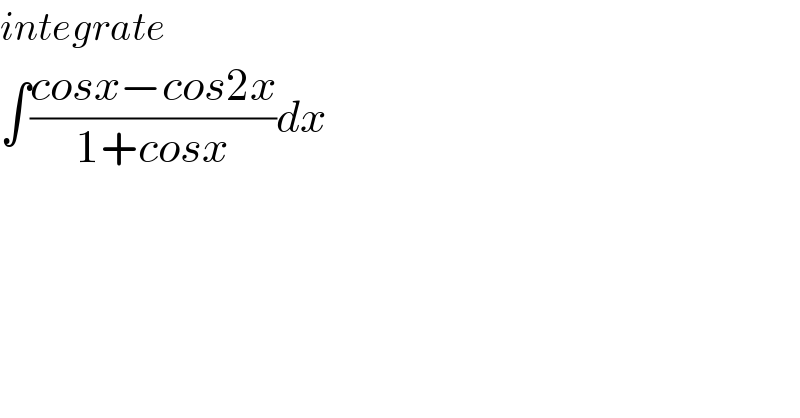
$${integrate} \\ $$$$\int\frac{{cosx}−{cos}\mathrm{2}{x}}{\mathrm{1}+{cosx}}{dx} \\ $$
Answered by $@ty@m last updated on 12/Oct/17

$$=\int\frac{{cosx}−\left(\mathrm{2}{cos}^{\mathrm{2}} {x}−\mathrm{1}\right)}{\mathrm{1}+{cosx}}{dx} \\ $$$$=\int\frac{\mathrm{1}+\mathrm{cos}{x}\:−\mathrm{2cos}\:^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{cos}\:{x}}{dx} \\ $$$$=\int\left(\mathrm{1}−\frac{\mathrm{2cos}\:^{\mathrm{2}} {x}}{\mathrm{1}+\mathrm{cos}\:{x}}\right){dx} \\ $$$$={x}−\int\:\:\frac{\mathrm{2}\left(\mathrm{2cos}\:\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$={x}−\int\left(\frac{\mathrm{2cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{1}}{\mathrm{cos}\:\frac{{x}}{\mathrm{2}}}\right)^{\mathrm{2}} {dx} \\ $$$$={x}−\int\left(\mathrm{2cos}\:\frac{{x}}{\mathrm{2}}−\mathrm{sec}\:\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} {dx} \\ $$$$={x}−\int\left(\mathrm{4cos}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−\mathrm{4}\right){dx} \\ $$$$={x}−\mathrm{2}\int\left(\mathrm{1}+\mathrm{cos}\:{x}\right){dx}−\int\mathrm{sec}\:^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}+\mathrm{4}\int{dx} \\ $$$$={x}−\mathrm{2}{x}−\mathrm{2sin}\:{x}−\mathrm{2tan}\:\frac{{x}}{\mathrm{2}}+\mathrm{4}{x}+{C} \\ $$$$=\mathrm{3}{x}−\mathrm{2sin}\:{x}−\mathrm{2tan}\:\frac{{x}}{\mathrm{2}}+{C}\:{Ans}. \\ $$
