integrate-e-x-2-x-2-dx-

Question Number 42182 by mondodotto@gmail.com last updated on 19/Aug/18

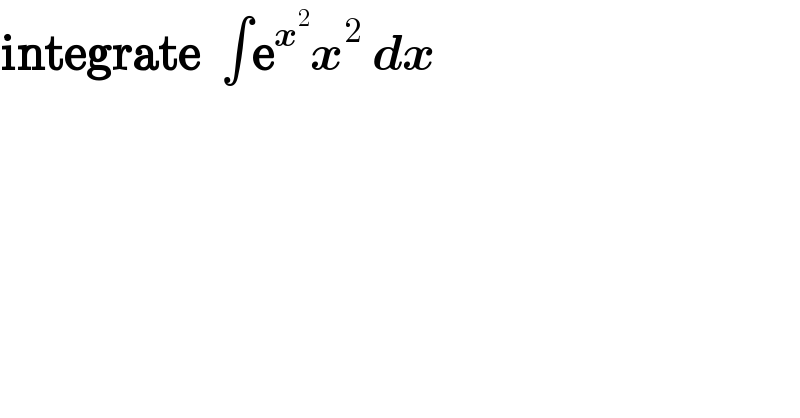
$$\boldsymbol{\mathrm{integrate}}\:\:\int\boldsymbol{\mathrm{e}}^{\boldsymbol{{x}}^{\mathrm{2}} } \boldsymbol{{x}}^{\mathrm{2}} \:\boldsymbol{{dx}} \\ $$

Commented by mondodotto@gmail.com last updated on 19/Aug/18

$$\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{help}}\:\boldsymbol{\mathrm{this}} \\ $$

Commented by maxmathsup by imad last updated on 19/Aug/18

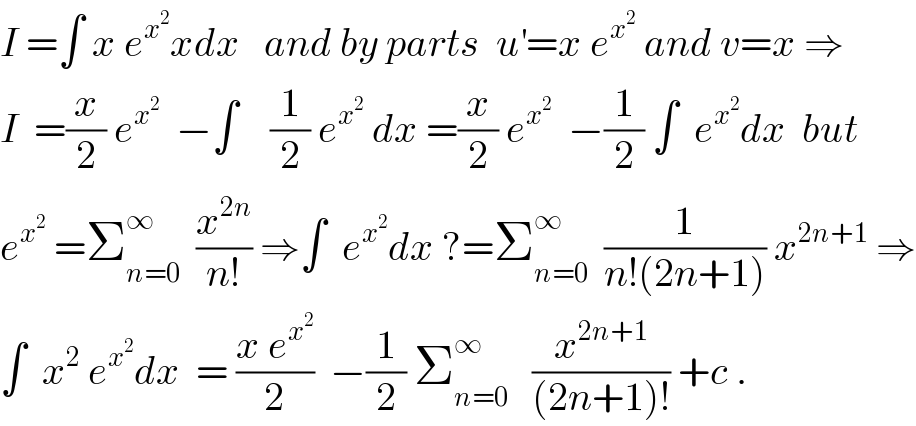
I =∫ x e^x^2 xdx and by parts u^′ =x e^x^2 and v=x ⇒ I =(x/2) e^x^2 −∫ (1/2) e^x^2 dx =(x/2) e^x^2 −(1/2) ∫ e^x^2 dx but e^x^2 =Σ_(n=0) ^∞ (x^(2n) /(n!)) ⇒∫ e^x^2 dx ?=Σ_(n=0) ^∞ (1/(n!(2n+1))) x^(2n+1) ⇒ ∫ x^2 e^x^2 dx = ((x e^x^2 )/2) −(1/2) Σ_(n=0) ^∞ (x^(2n+1) /((2n+1)!)) +c .

$${I}\:=\int\:{x}\:{e}^{{x}^{\mathrm{2}} } {xdx}\:\:\:{and}\:{by}\:{parts}\:\:{u}^{'} ={x}\:{e}^{{x}^{\mathrm{2}} } \:{and}\:{v}={x}\:\Rightarrow \\ $$$${I}\:\:=\frac{{x}}{\mathrm{2}}\:{e}^{{x}^{\mathrm{2}} } \:\:−\int\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{{x}^{\mathrm{2}} } \:{dx}\:=\frac{{x}}{\mathrm{2}}\:{e}^{{x}^{\mathrm{2}} } \:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:{e}^{{x}^{\mathrm{2}} } {dx}\:\:{but}\: \\ $$$${e}^{{x}^{\mathrm{2}} } \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{{x}^{\mathrm{2}{n}} }{{n}!}\:\Rightarrow\int\:\:{e}^{{x}^{\mathrm{2}} } {dx}\:?=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{x}^{\mathrm{2}{n}+\mathrm{1}} \:\Rightarrow \\ $$$$\int\:\:{x}^{\mathrm{2}} \:{e}^{{x}^{\mathrm{2}} } {dx}\:\:=\:\frac{{x}\:{e}^{{x}^{\mathrm{2}} } }{\mathrm{2}}\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)!}\:+{c}\:. \\ $$

Commented by maxmathsup by imad last updated on 19/Aug/18

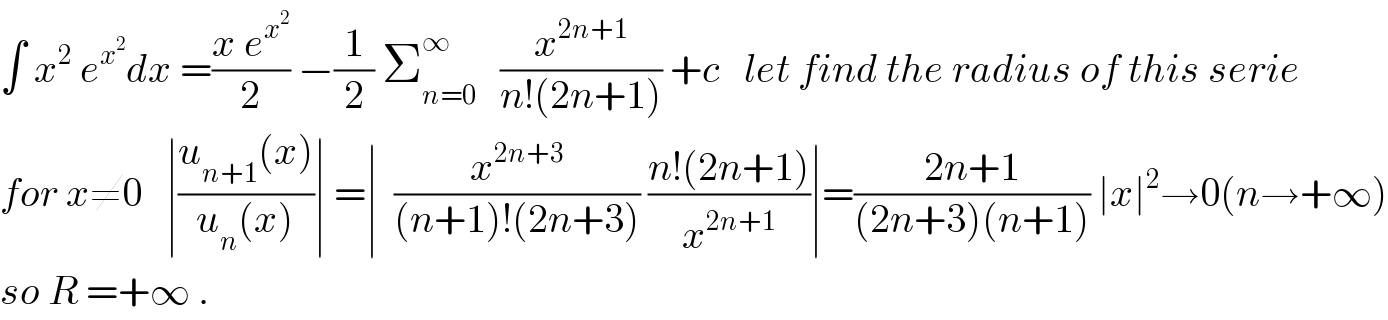
∫ x^2 e^x^2 dx =((x e^x^2 )/2) −(1/2) Σ_(n=0) ^∞ (x^(2n+1) /(n!(2n+1))) +c let find the radius of this serie for x≠0 ∣((u_(n+1) (x))/(u_n (x)))∣ =∣ (x^(2n+3) /((n+1)!(2n+3))) ((n!(2n+1))/x^(2n+1) )∣=((2n+1)/((2n+3)(n+1))) ∣x∣^2 →0(n→+∞) so R =+∞ .

$$\int\:{x}^{\mathrm{2}} \:{e}^{{x}^{\mathrm{2}} } {dx}\:=\frac{{x}\:{e}^{{x}^{\mathrm{2}} } }{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}\:+{c}\:\:\:{let}\:{find}\:{the}\:{radius}\:{of}\:{this}\:{serie} \\ $$$${for}\:{x}\neq\mathrm{0}\:\:\:\mid\frac{{u}_{{n}+\mathrm{1}} \left({x}\right)}{{u}_{{n}} \left({x}\right)}\mid\:=\mid\:\:\frac{{x}^{\mathrm{2}{n}+\mathrm{3}} }{\left({n}+\mathrm{1}\right)!\left(\mathrm{2}{n}+\mathrm{3}\right)}\:\frac{{n}!\left(\mathrm{2}{n}+\mathrm{1}\right)}{{x}^{\mathrm{2}{n}+\mathrm{1}} }\mid=\frac{\mathrm{2}{n}+\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)\left({n}+\mathrm{1}\right)}\:\mid{x}\mid^{\mathrm{2}} \rightarrow\mathrm{0}\left({n}\rightarrow+\infty\right) \\ $$$${so}\:{R}\:=+\infty\:. \\ $$

Facebook Tweet Pin

integrate-e-x-2-x-2-dx-

Leave a Reply Cancel reply